16.2a - Line Integrals Of Scalar Fields

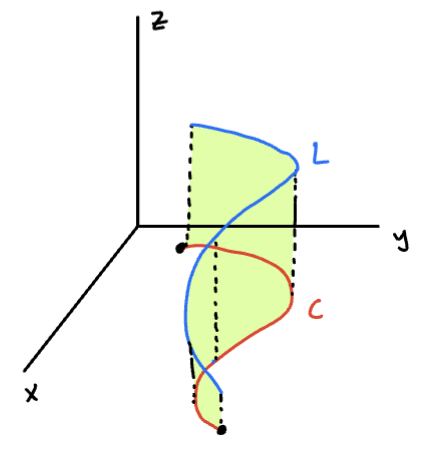
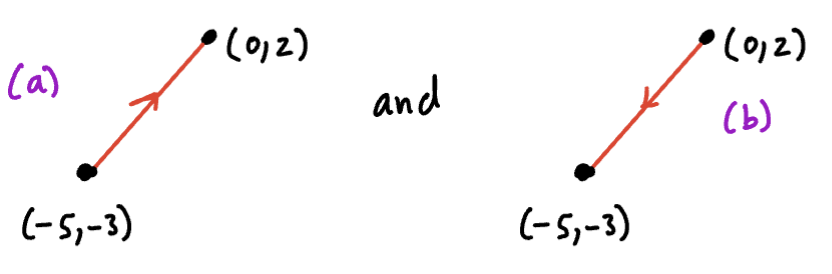Suppose the curve $C$ in the xy-plane has the vector equation $\vec{r}(t)=⟨x(t),y(t)⟩$. Suppose $C$ lies below the surface $z=f(x,y)$, and consider the problem of find the area of the “sheet” between the $C$ and the surface.

Sketch

• $C$ is a curve in the xy-plane
• The blue space curve $L$ lives on the surface $z=f(x,y)$. It is the curve obtained by lifting $C$ to the surface
• WE seek the area of the sheet between $C$ and $L$.

We proceed the dividing $C$ into n sub-arcs. This is achieved by sub-dividing the parameter interval $[a,b]$ into n sub-intervals of width $\Delta t=\frac{(b-a)}{n}$.

Sketch

The point $t_i$ in the parameter interval corresponds to the point on $C$ with position vector $P_i=⟨x(t_i),y(t_i)⟩$

Let $\Delta {\partial }_i$ denote the length of the sub-arc between $P_i$ and $P_{i-1}$.

Then:

The area of the portion of the sheet above $\Delta {\partial }_i$ is approximately the area of the rectangle whose width is the length of $\Delta {\partial }_i$, and whose height is $f(x,y)$ evaluated at $P_i$. We obtain the area of the sheet by summing up all of these smaller portions of the sheet:

$$AreaofSheet=\sum _{i=1}^{n}f(x(t_i),y(t_i))\Delta {\partial }_i$$

¹

But we already know $\Delta \partial i$ is the arc length differential(see section 13.3a)

$$\Delta \partial i=\sqrt{(\dot{x}(t_i){)}^2+(\dot{y}(t_i){)}^2}\Delta t$$

²

where the “dot” notation means “derivative with respect to t”, i.e. $\dot{x}=\frac{dx}{dt}$. Substituting ² into ¹ and taking the limit $n\to \infty$ yields an integral:

$$AreaofSheet={\int }_a^{b}f(x(t),y(t))\sqrt{{\dot{x}}^2+{\dot{y}}^2}dt$$

This particular integral is called the Line Integral:

Definition

If $f$ is defined on the curve $C$ given by $\vec{r}(t)=⟨x(t),y(t)⟩$, $t\in [a,b]$, then the line integral of $f$ along $C$ is:

$${\int }_{C}f(x,y)d\partial ={\int }_a^{b}f(x(t),y(t))\sqrt{{\dot{x}}^2+{\dot{y}}^2}dt$$

---

Remarks

1. When the differential is $d\partial$, this is called the line integral with respect to arc length. We will see other types of line integrals later on in this lecture.
2. The expression on the left hand side tells us what a line integral means: add up all the length elements $d\partial$ and multiply by their heights.
3. Cleaning up notation: If $\vec{r}(t)=⟨x(t),y(t)⟩$, then $|\vec{r}(t)|=\sqrt{{\dot{x}}^2+{\dot{y}}^2}$, so we get:

$${\int }_{C}f(x,y)d\partial ={\int }_a^{b}f(\vec{r}(t))\cdot |{\vec{r}}^{\prime }(t)|dt$$

---

Examples

Example

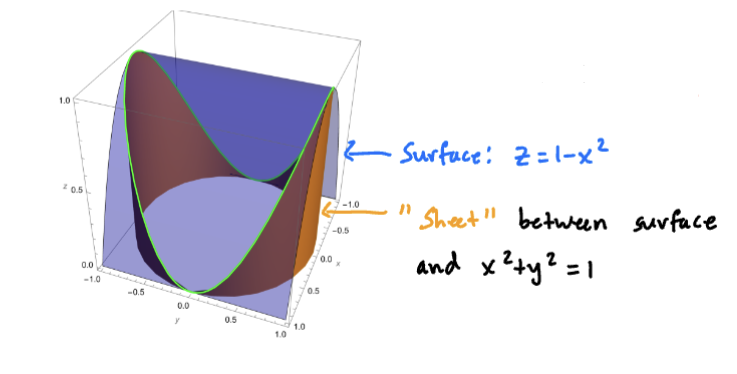
Find the area of the surface extending upward from the circle $x_{6}2+y^2=1$ in the xy-plane to the parabolic cylinder $z=1-x^2$

Solution

We are finding the area of the “sheet” between the surface $z=1-x^2$ and the circle $x^2+y^2=1$ in the xy-plane. We therefore seek the line integral ${\int }_{C}d\partial$, where $C$ is the unit circle and $f(x,y)=1-x^2$

Sketch

Now we know what we are looking for, let’s go through the steps to evaluate:

1. Parameterize $C$
   • This is done by $\vec{r}(t)=⟨\cos t,\sin t⟩$, $t\in [0,2\pi ]$
2. Compute the Arc Length differential

$$d\partial =|{\vec{r}}^{\prime }(t)|dt=|⟨-\sin t,\cos t⟩|dt$$ $$=\sqrt{{\sin }^{2}t+{\cos }^{2}t}dt=dt$$

3. Evaluate the line integral

$${\int }_{C}f(x,y)d\partial ={\int }_0^{2\pi }(1-x^2)d\partial$$ $${\int }_0^1{\int }_0^1\frac{1}{1-xy}dxdy=\sum _{n=1}^{\infty }\frac{1}{n^2}$$

substitute in $d\partial =dt$ and $x=\cos t$

$$={\int }_0^{2\pi }(1-{\cos }^{2}t)dt$$ $$={\int }_0^{2\pi }{\sin }^{2}tdt=\frac{1}{2}{\int }_0^{2\pi }1-\cos 2tdt$$

remark: ${\int }_0^{2\pi }{\sin }^2\theta d\theta ={\int }_0^{2\pi }{\cos }^2\theta d\theta =\pi$

$$=\left(\frac{1}{2}\right)(2\pi )=\pi$$

---

Line Integrals in Space

The concept of a Line Integral can be extended to space curves of the form $\vec{r}(t)=⟨x(t),y(t),z(t)⟩$, $t\in [a,b]$:

$${\int }_{C}f(x,y,z)d\partial ={\int }_a^{b}f(x(t),y(t),z(t))\sqrt{{\dot{x}}^2+{\dot{y}}^2+{\dot{z}}^2}dt$$ $$={\int }_a^{b}f(\vec{r}(t))|{\vec{r}}^{\prime }(t)|dt$$

The analogy of the “area of the sheet” is now difficult because the “height” of the sheet is now in 4D. Instead, we can interpret the line integral as the mass of a thin wire with shape $C$ and linear density function $f(x,y,z)$

why? Because:

$$(LinearDensity)=\frac{mass}{length}\to mass=(Density)(Length)$$

In the expression ${\int }_{C}f(x,y,z)d\partial$, $d\partial$ represents the length of a small piece of wire; so, if $f$ is density, $f\cdot d\partial$ is the mass of that piece. The integrand sign means “add up all the mass elements,” yielding the total mass.

Example

A helix-shaped wire described by $\vec{r}(t)=⟨\cos t,\sin t,t⟩$, $t\in [0,2\pi ]$, has linear density function $f(x,y,z)=y\sin z$. Find the mass of the wire.

Solution

We seek the line integral ${\int }_{C}y\sin zd\partial$, where $C$ is the helix. The arc length differential is:

$$d\partial =\sqrt{{\dot{x}}^2+{\dot{y}}^2+{\dot{z}}^2}dt=\sqrt{{\sin }^{2}t+{\cos }^{2}t+1}dt=\sqrt{2}dt$$

The line integral (and mass) is therefore:

$${\int }_{C}y\sin zd\partial ={\int }_0^{2\pi }{\sin }^{2}t\cdot \sqrt{2}dt=\sqrt{2}\pi$$

---

Line Integrals with respect to X, Y, or Z

So far, we have defined the line integral with respect to arc length, $d\partial$. Now we define the line integral with respect to $x,y,orz$:

$${\int }_{C}f(x,y,z)dx={\int }_a^{b}f(x,y,z)\dot{x}(t)dt,$$ $${\int }_{C}f(x,y,z)dy={\int }_a^{b}f(x,y,z)\dot{y}(t)dt,$$ $${\int }_{C}f(x,y,z)dz={\int }_a^{b}f(x,y,z)\dot{z}(t)dt.$$

Remarks

1. To obtain the formulae on the right, we observe:

$$\dot{x}(t)=\frac{dx}{dt}\to dx=\dot{x}(t)dt$$

2. The geometric interpretation is less intuitive than the line integral with respect to arc length. The line integral with respect to x, for example, can be interpreted as the area of the projection of the sheet onto the xz-plane ( see the beginning for the sheet sketch, and then imagine that pushing against the xz-plane).
3. The utility of this type of integral will become apparent when we study line integrals of vector fields; for now, we are learning the mechanics of working with them.

Example

Evaluate ${\int }_C{y}^{2}dx+{\int }_{C}xdy$ for the following paths: a. $c$ is the line segment from $(-5,-3)$ to $(0,2)$ b. $c$ is the line segment from $(0,2)$ to $(-5,-3)$ c. $c$ is the arc of the parabola $x=4-y^2$ from $(-5,-3)$ to $(0,2)$.

Remark

Linearity holds for line integrals so it will be easier to find

$${\int }_C{y}^{2}dx+xdy$$

Which is only one integral instead

A.

We need to find a vector parameterization of the segment. Recall that the line segment joining ${\vec{r}}_0=⟨x_0,y_0⟩$ and ${\vec{r}}_1=⟨x_1,y_1⟩$ is $\vec{r}(t)=(1-t){\vec{r}}_0+t{\vec{r}}_1$, where $t\in [0,1]$. So, we get:

$$\begin{array}{rl}\vec{r}(t)& =(1-t)⟨-5,-3⟩+t⟨0,2⟩\\ & =⟨-5+5t,-3+3t⟩+⟨0,2t⟩\\ & =⟨-5+5t,-3+5t⟩\\ & =⟨x(t),y(t)⟩\end{array}$$

Therefore:

$$\begin{array}{rl}{\int }_C{y}^{2}dx+xdy& ={\int }_0^1(-3+5t{)}^2(5)+(-5+5t)(5)dt\\ & =5{\int }_0^{1}9-30t+25t^2-5+5t\\ & =5{\int }_0^{1}25t^2-25t+4dt\\ & =-\frac{5}{6}\end{array}$$

B.

This is the same path, but we have reversed direction:

We start at $(0,2)$ and end at $(-5,-3)$, so:

$$\begin{array}{rl}\vec{r}(t)& =(1-t)⟨0,2⟩+t⟨-5,-3⟩\\ & =⟨0,2-2t⟩+⟨-5t,-3t⟩\\ & =⟨-5t,2-5t⟩=⟨x(t),y(t)⟩,t\in [0,1]\end{array}$$

Therefore, the line integral is:

$$\begin{array}{rl}{\int }_C{y}^{2}dx+xdy& ={\int }_0^1(2-t_5{)}^2(-5)+(-5t)(5)dt\\ & =-5{\int }_0^1(2-5t{)}^2-5tdt\\ & =-5{\int }_0^{1}4-20t+25t^2-5t\\ & =-5{\int }_0^{1}25t^2-25t+4dt\\ & =\frac{5}{6}\end{array}$$

C.

Parameterize the parabola by $x=4-y^2$, $y=y$, $y\in [-3,2]$:

$$\begin{array}{rl}{\int }_C{y}^{2}dx+xdy& ={\int }_{-3}^2{y}^2(-2y)+(4-y^2)(1)dy\\ & ={\int }_{-3}^2-2y^2+4-y^{2}dy\\ & =\frac{245}{6}\end{array}$$

---

Properties of Line Integrals

1. A parameterization $\vec{r}(t)$ of $C$ comes with an orientation. In the previous example A and B, we had:

Sketch

If $-C$ denotes $C$ but traversed “backwards”, then the previous example suggests:

$${\int }_{-C}f(x,y)dx=-{\int }_{C}f(x,y)dx$$

³

i.e. reversing the orientation of $C$ flips the sign of the line integral. ( This is the same idea as reversing the order of integration; one way, the $\Delta x$ values are negative. )

Note

³ is true for the line integral with respect to $x,y,orz$, but not with respect to arc length. This is because arc length is independent of the orientation of the path; always a positive quantity

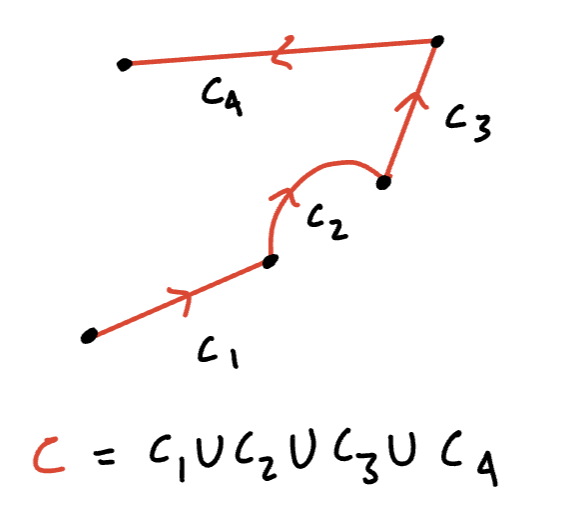
2. Suppose $C$ is a finite union of paths.

Sketch

To find ${\int }_{C}fd\partial$ (or dx), we add up the line integral of each piece, e.g.

$${\int }_{C}fd\partial ={\int }_{C_1}fd\partial +{\int }_{C_2}fd\partial +\cdots +{\int }_{C_4}fd\partial$$

---

Footnotes

1. Area of Sheet Formula ↩ ↩²

2. Arc Length Differential ↩ ↩²

3. Inverse Line Integral ↩ ↩²