15.8 - Triple Integrals in Spherical Coordinates

The spherical coordinates $(\rho ,\varphi ,\theta )$ of a point P in space have the following meaning:

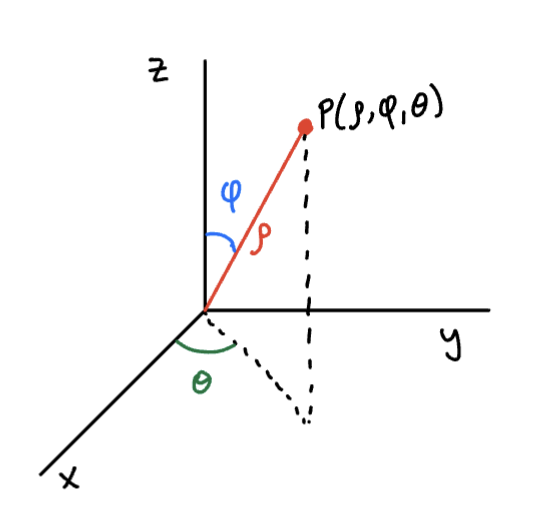
Sketch

Where:

• $\rho$ is the distance from the origin to P ($\varphi \ge 0$)
• $\theta$ is the polar angle in the xy-plane ($0\le \theta \le 2\pi$)
• $\varphi$ is the angle between the z-axis and the segment from the origin to P ($0\le \varphi \le \pi$)

Remark

$\varphi$ ranges from $0$ to $\pi$. Because $\theta$ ranges from $0$ to $2\pi$, we can always capture the “left” side of the yz-plane.

Examples of Surfaces in Spherical Coordinates

1. $\rho =c$ represents a sphere of radius $c$. Distance from the pole is fixed; $\varphi$ and $\theta$ sweep out the sphere.
2. $\varphi =c$ represents a cone. Angle between the cone and z-axis are fixed; $\theta$ sweeps out the cone and $\rho$ stretches it.

---

Conversion Formulae: Spherical to Cartesian

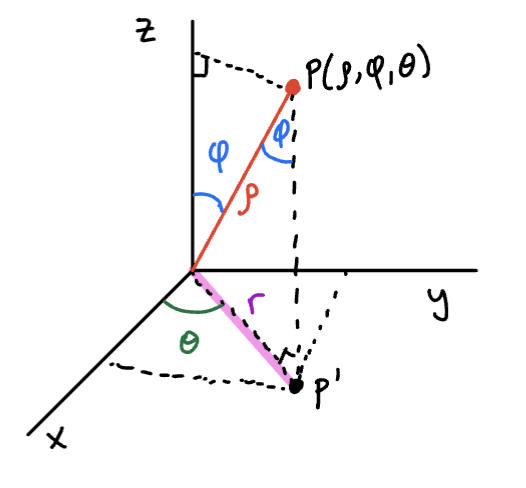
Sketch

Let $p^{\prime }$ be the projection of $P$ onto the xy-plane. The $x$ and $y$ coordinates of $P^{\prime }$ ( and hence $P$ ) are described in polar coordinates by:

$$x=r\cos \theta ,y=r\sin \theta (\ast )$$

where $r$ is the distance from the origin to $p^{\prime }$.

Observe

$$\sin \varphi =\frac{r}{\rho }\to r=\rho \sin \varphi \to substitutinginto(\ast ):$$ $$x=\rho \sin \varphi \cos \theta ,y=\rho \sin \varphi \sin \theta$$

From the figure, we also see:

$$\cos \varphi =\frac{z}{\rho }\to z=\rho \cos \varphi$$

Because $\rho$ is the distance from the point to the origin:

$${\rho }^2=x^2+y^2+z^2$$

Another useful conversion:

$$x^2+y^2=r^2={\rho }^2{\sin }^2\varphi$$

Summary: Spherical Conversion Formulae

$$x=\rho \sin \varphi \cos \theta ,y=\rho \sin \varphi \sin \theta ,z=\rho \cos \varphi ,$$ $$x^2+y^2+z^2={\rho }^2$$ $$x^2+y^2-{\rho }^2{\sin }^2\varphi$$

---

Triple Integrals in Spherical Coordinates

Suppose $E$ is a region described conveniently in spherical coordinates:

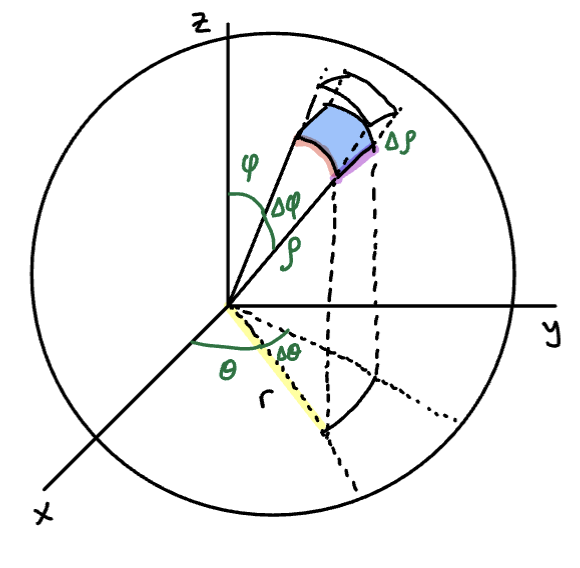
Sketch

The $volumeelementdV$ is a “spherical wedge” whose face we have shaded in blue. The volume of this wedge is:

$$dV=(AreaofFace)\cdot Height=(AreaofFace)\Delta \rho$$

We can approximate the area of the face by:

$$AreaofFace=Width\cdot Length$$

The $width$ is the length of the circular arc with angle $\Delta \varphi$ and radius $\rho$:

$$Width=\rho \Delta \varphi$$

The $length$ is the length of the circular arc with angle $\Delta \theta$ and radius $r=\rho \sin \varphi$. (We determined this on the previous part.) So, $length=\rho \sin \varphi \Delta \theta$

Putting it all together:

$$dV=(AreaofFace)\cdot Height$$ $$=Length\cdot Width\cdot Height$$ $$=(\rho \sin \varphi \Delta \theta )\cdot (\rho \Delta \varphi )\cdot \Delta \rho$$ $$={\rho }^2\sin \varphi \Delta \rho \Delta \varphi \Delta \theta \to {\rho }^2\sin \varphi d\rho d\varphi d\theta$$

Where ${\rho }^2\sin \varphi d\rho d\varphi d\theta$ is the $SphericalVolumeElement$

The triple integral formula is then:

$$\int {\int }_E\int f(x,y,z)dV={\int }_{{\theta }_1}^{{\theta }_2}{\int }_{{\varphi }_1}^{{\varphi }_2}{\int }_{{\rho }_1}^{{\rho }_2}f(x,y,z){\rho }^2\sin \varphi d\rho d\varphi d\theta$$

---

Examples

Example

Use spherical coordinates to find the volume of the solid that lies above the cone $z=\sqrt{x^2+y^2}$ and below the sphere $x^2+y^2+z^2=z$

Solution

By completion of the square:

$$x^2+y^2+z^2-z=0\to x^2+y^2+{\left(z-\frac{1}{2}\right)}^2=\frac{1}{4}$$

The sphere has center $\left(0,0,\frac{1}{2}\right)$ and radius $\frac{1}{2}$.

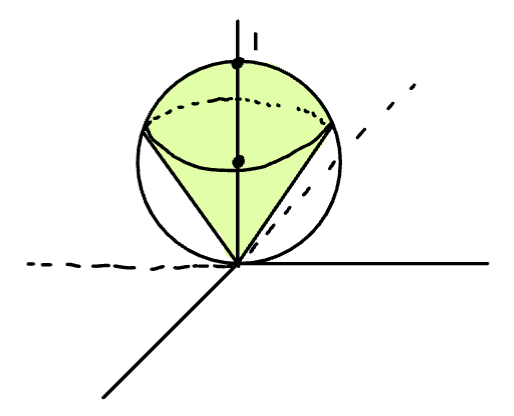
Sketch

“Ice Cream Cone” region

To determine bounds on $\rho ,\varphi ,\theta$, express the surfaces in spherical coordinates:

$$Sphere:x^2+y^2+z^2=z\to {\rho }^2=\rho \cos \varphi$$ $$\to \rho =\cos \varphi$$ $$Cone:z=\sqrt{x^2+y^2}\to \rho \cos \varphi =\sqrt{{\rho }^2{\sin }^2\varphi }$$