Exercise 01
Examine the formal definition of a Turing Machine to answer the following questions, and explain your reasoning.
-
Can a Turing machine ever write the blank symbol on its tape?
- Yes, a Turing machine can write the blank symbol on its tape as part of its operation.
-
Can the tape alphabet be the same as the input alphabet ?
- No, the tape alphabet must include the blank symbol while doesn’t.
-
Can a “plain vanilla” Turing machine’s head ever be in the same location in two successive steps?
- No, because “plain vanilla” cannot stay in one place, it has to move left or right.
-
Can a Turing machine contain just a single state?
- No, a Turing machine needs at least two states (initial state and accept/reject).
Exercise 02
For the following Turing Machine, complete the questions below:
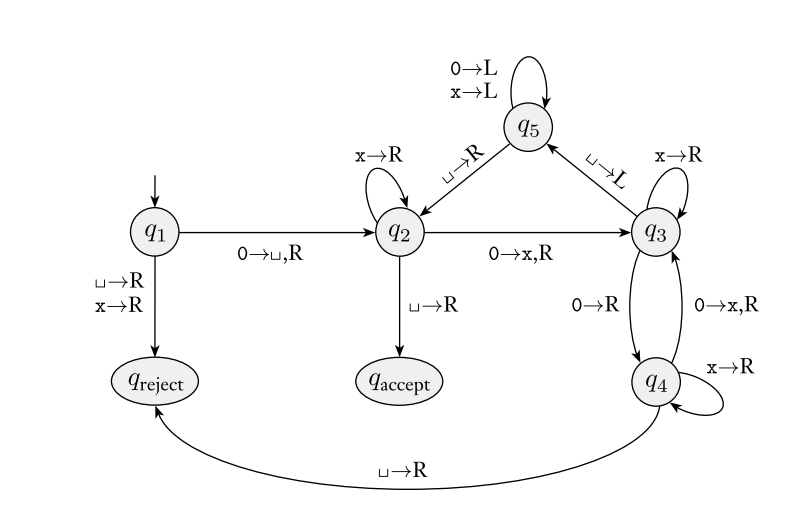
- Work out the complete sequence of configurations which would result if the input were 000
- Check: did you end in ?
- Yes, we did.
Exercise 03
Given some Turing machine, , we observe that configuration yields configuration . Give the piece of the transition function, , which makes this possible.
How about the case where configuration yields ?
How about the case where yields ?
Exercise 04
Given the Turing machine shown in Sipser ITTTOC Example 3.9, write the complete sequence of configurations that formally describes the computation on the following inputs:
![]()
- 01#01
Transisitons
q1 01#01 → x q3 1#01 → x1 q3 #01 → x1# q5 01 →
x1# q6 x1 → x1 q7 #x1 → x q7 1#x1 → x q1 1#x1 →
xx q3 #x1 → xx# q5 x1 → xx# q6 xx → xx q7 #xx →
x q7 x#xx → x q8 x#xx → xx# q_accept xx
Accept
- 00#10
Transisitons
q1 00#10 → x q3 0#10 → x0 q3 #10 → x0# q5 10 →
x0# q6 x0 → x0 q7 #x0 → x q7 0#x0 → x q1 0#x0 →
xx q3 #x0 → xx# q5 x0 → xx# q6 xx → xx q7 #xx →
x q7 x#xx → q7 xx#xx → q_reject xx#xx
Reject
Which of these halt in the accept state, and which halt in the reject state?
We can see that the first input halts in the accept state, while the second input halts in the reject state.