Double Integrals Practice

Problem 1

$\int {\int }_{R}4-2ydA,R=[0,1]\times [0,1]$

What does this problem mean?

The volume beneath the the surface AND above this region

Sketching this graph in the 3d, we map the 2d line as a plane

![[Screenshot 2024-10-07 at 3.15.20 PM.png]]

Attemping to calculate this without the integral, we can ge tthe sides of the shape to find the area of each element

splitting the element into two pieces, the rectangle and the triangle

another problem

$\int \int \sqrt{9-x^2}dA,R=[-3,3]\times [0,4]$

plotting in the 3d:

we get this graph by simplifying the equation:

$z=\sqrt{9-x^2}$ $z^2=9-x^2$ $x^2+z^2=9$

The point we are trying to get at is that we dont necessarily have to evaluate the double integrals, as if we can graph them we can apply an equation like the cylinder formula, in this case, to solve

$Volume=\frac{\pi r^{2}h}{2}$ Plugging it in:

$=\frac{\pi \ast 3^2\ast 4}{2}$ which evaluates to

$=18\pi$

15.1 problem

${\int }_0^{\frac{\pi }{3}}{\int }_0^{\frac{\sqrt{\pi }}{3}}\frac{\tan \theta }{\sqrt{1-t^2}}dtd\theta$

type 1 solve:

$\int \frac{\tan \theta }{\sqrt{1-t^2}}dt=\tan \theta \ast \arcsin t$

$=\tan \theta (\arcsin )$

$\frac{\pi }{3}\ln |\sec \frac{\pi }{3}|-\frac{\pi }{3}\ln |\sec 0|$ $\frac{\pi }{3}\ln (2)-\frac{\pi }{3}\ln (1)=\frac{\pi }{3}\ln (2)$

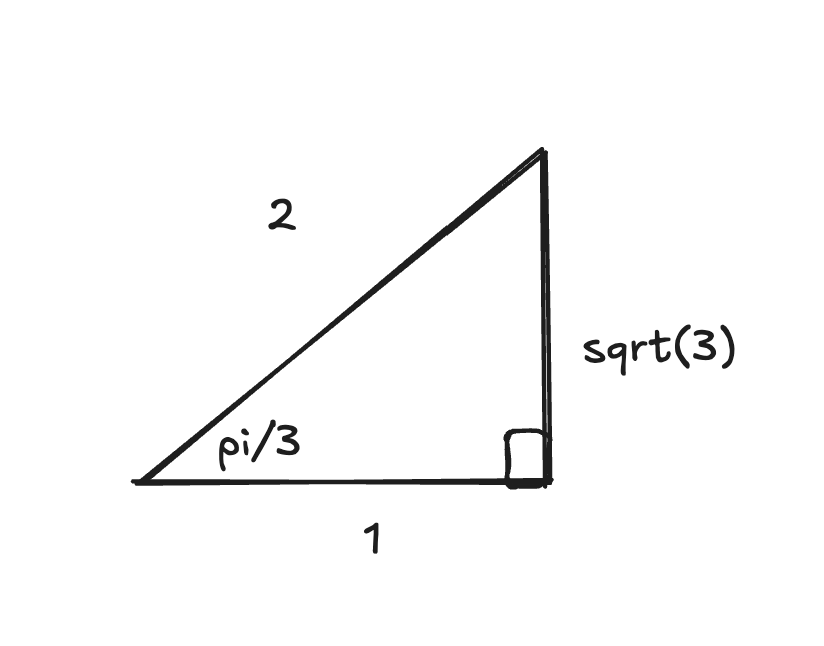
anohter one

$2x+y+z=10$

How to solve:

Set 2 of the variables equal to 0

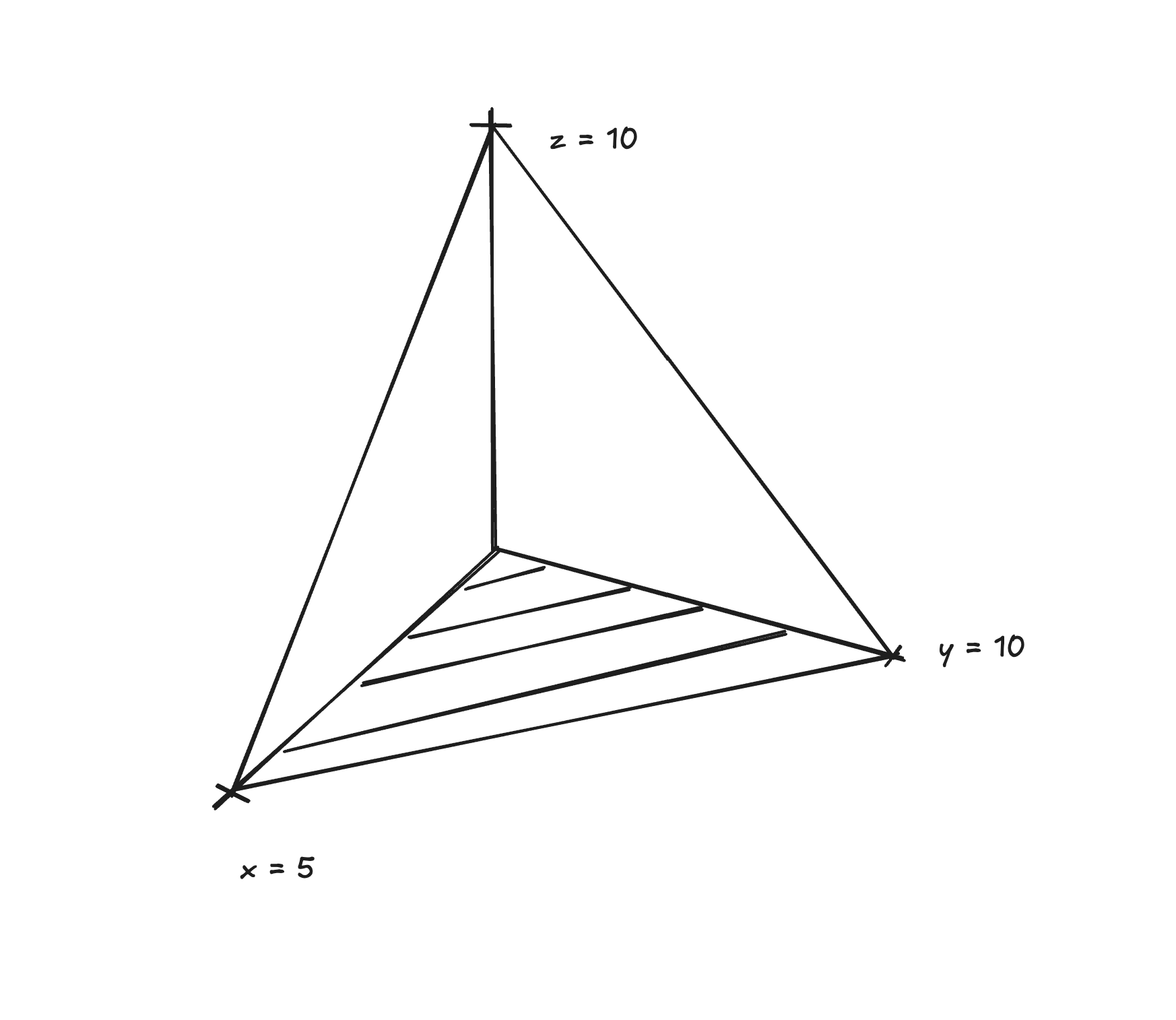
bringing into 2d

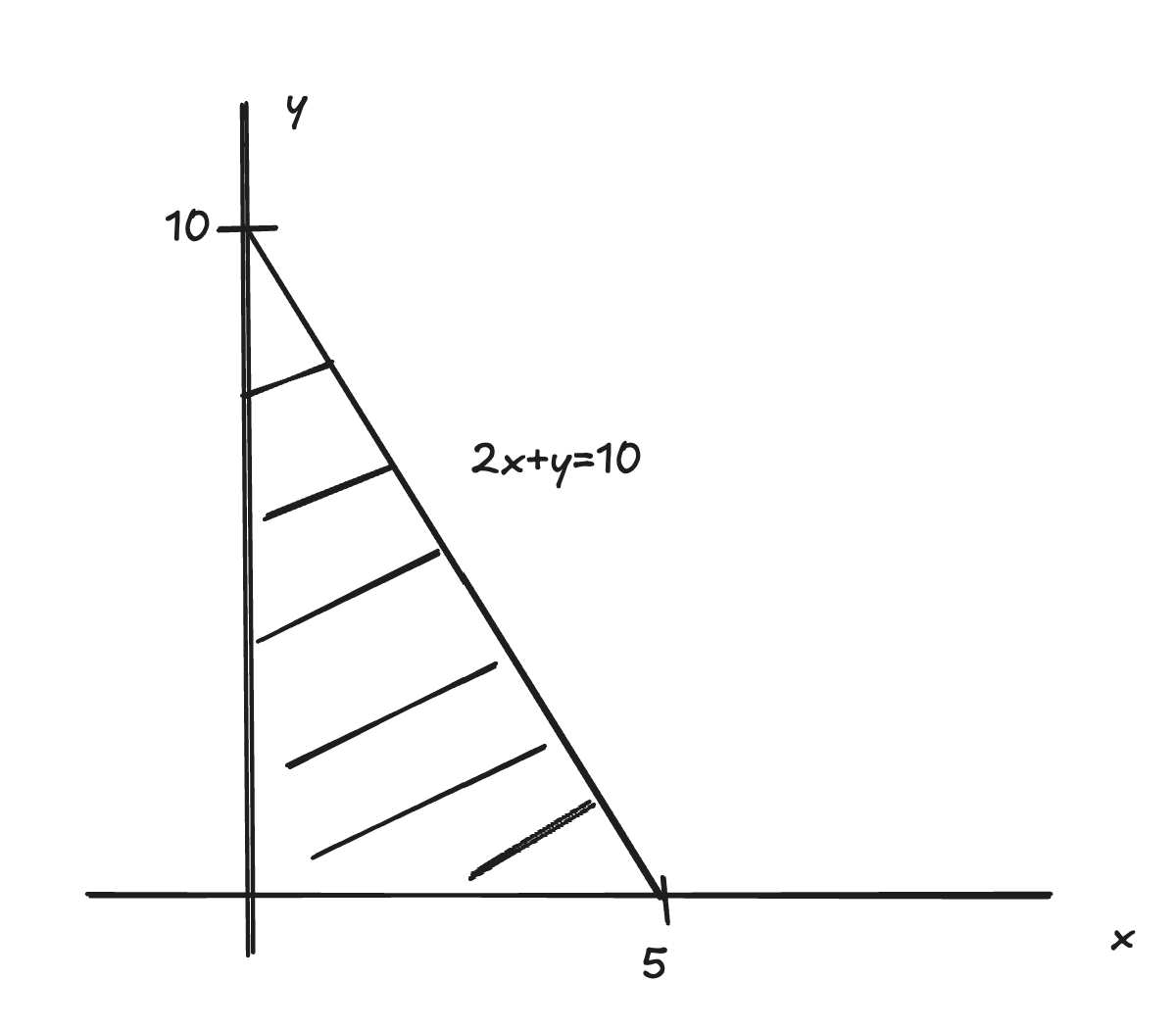
setting up the integral

we are finding the volume between d and the surface

we can write this as

$z=10-2x-y$ setting it up wiht type 1 we get

${\int }_0^5{\int }_0^{10-2x}10-2x-ydydx$

we can rewrite the 2d line in terms of y to get

$x=5-\frac{2}{y}$ if you wanted to solve for type to

solving type 1

I 1 ${\int }_0^{10-2x}10-2x-ydx={10y-2xy-\frac{y^2}{2}|}_0^{10-2x}$

$10(10-2x)-2x(10-2x)-\frac{(10-2x{)}^2}{2}$ $=(10-2x)\left[10-2x-\frac{1}{2}(10-2x)\right]$ $=(10-2x)(10-2x-5+x)$ solving via FOIL $=(10-2x)(5-x)=250-250+\frac{250}{3}$

solving by parts

## double integral problem $$\int_{0}^1 \int_{\arcsin y}^{\frac{\pi}{2}} \cos x \sqrt{ 16+\cos^2x } \ dx \ dy$$ set arcsiny = x set pi/2 = x $$x = \arcsin y \rightarrow \sin x = y$$ setting up the integral again with this information $$\int \int_{0}^{\sin x} \cos x \sqrt{ 16+\cos^2 x } \ dy \ dx$$ integrate with respect to y: no y's so we just add one y at the begginging $$\left. y\cos x\sqrt{ 16+\cos^2 x } \right|_{0=y}^{\sin x=y}$$ y is replaced by sin x for the integration limits $$\sin x\cos x\sqrt{ 16+\cos^2 }$$ $$\int _{0}^{\frac{\pi}{2}} \sin x \cos x\sqrt{ 16+\cos^2x } \ dx$$ $$u = 16+\cos^2x$$ $$du = -2\sin x\cos x \ dx$$ $$-\frac{1}{2} du = \sin x\cos x \ dx$$ $$- \int_{0}^1 u \sqrt{ 16+u^2 } \ du$$ trig sub $$u = 4\tan \theta$$ $$du = 4\sec^2 \theta \ d\theta$$ $$\int 4 \tan \theta \cdot \sqrt{ 16+16\tan^2 \theta \cdot 4\sec^2\theta } \ d \theta$$ $$64 \int \tan \theta \cdot \sec^3 \theta \ d\theta$$ $$\int \tan \theta \cdot (\tan^2 \theta + 1 ) \ \sec \theta$$ $$64 \int \tan \theta \cdot \sec \theta \cdot \sec^2 \theta \ d \theta$$ $$v = \sec \theta, \ \ \ 64 \int v^2 dv = \frac{64v^3}{3}$$ ## anotha one $$\int \int_{R} ye ^ { -xy} \ dA \ , \ \ \ R = [0,2] \times [ 0,3]$$ $$\int_{0}^3 \int_{0}^2 ye ^{-xy} dx dy$$ $$\int _{0}^2 ye ^ {-xy} dx = \int - e^u du$$ $$u = -xy \ \ \ \ du = -ydx$$ $$= \left. -e^u \right|_{0}^{-2y}$$ $$3 - \int_{0}^3 e^{-2y} dy$$ $$u = -2y$$ $$du = -2dy$$ $$ $$