15.3 - Double Integrals in Polar Coordinates

Many integration regions can be described conveniently in polar coordinates. Recall the meaning of the polar coordinate $(r, θ)$

MatPlotLib Example

Python

import matplotlib.pyplot as plt
import numpy as np

# Values for demonstration (r = distance, theta = angle in radians)
r = 5  # radial distance
theta = np.pi / 4  # 45 degrees

# Convert from polar to cartesian coordinates
x = r * np.cos(theta)
y = r * np.sin(theta)

# Create figure and axis
fig, ax = plt.subplots()

# Plot the line representing (r, theta)
ax.plot([0, x], [0, y], 'brown', label=r'$\theta$ line')
ax.plot([x, x], [0, y], 'k--')  # dashed line representing height (y)
ax.plot([0, x], [y, y], 'k--')  # optional horizontal line for x

# Plot the point at (r, theta)
ax.plot(x, y, 'bo')  # blue point at the end

# Annotations for polar coordinates (r, θ)
ax.annotate(r'$r = \mathrm{Distance\ from\ Pole}$', xy=(x / 2, y / 2), xytext=(-5, 1.5),
            textcoords='offset points', fontsize=12, color='brown')
ax.annotate(r'$\theta = \mathrm{Polar\ Angle}$', xy=(x / 2, y / 2), xytext=(15, -10),
            textcoords='offset points', fontsize=12, color='purple')

# Annotations for Cartesian coordinates (x, y)
ax.annotate(r'$(r, \theta)$', xy=(x, y), xytext=(5, 5),
            textcoords='offset points', fontsize=12, color='blue')
ax.annotate(r'$x$', xy=(x, 0), xytext=(5, -10), textcoords='offset points', fontsize=12)
ax.annotate(r'$y$', xy=(0, y), xytext=(-15, 0), textcoords='offset points', fontsize=12)

# Set axis limits and labels
ax.set_xlim(0, r + 1)
ax.set_ylim(0, r + 1)
ax.set_aspect('equal', 'box')

# Axes labels
ax.set_xlabel('x')
ax.set_ylabel('y')

# Add the origin label
ax.text(-0.5, -0.5, 'Pole / Origin', fontsize=10)

# Show the grid and plot
ax.grid(True)
plt.title('Polar Coordinates vs Cartesian Coordinates')
plt.show()

Output

Relationship to Cartesian:

$x = r cos θ$

$y = r sin θ$

$x^{2} + y^{2} = r^{2}$

Polar Coordinate Examples

Here are some sketched examples of polar coordinates:

Sketch

The disk $x^{2} + y^{2} \geq 1; {(r, θ) : 0 \leq r \leq 1, 0 \leq θ \leq 2 π}$
The semi-annulus $1 \leq x^{2} + y^{2} \leq 4; {(r, θ) : 1 \leq r \leq 2, 0 \leq θ \leq π}$
The disk $(x - 1)^{2} + y^{2} \leq 1; {(r, θ) : 0 \leq r] l e q 2 cos θ, \frac{- π}{2} \leq θ \leq \frac{π}{2}}$

The circle in the third example is given by:

Expanding and Simplifying:

(x - 1)^{2} + y^{2} = 1 \to x^{2} - 2 x + 1 + y^{2} = 1

\to x^{2} + y^{2} = 2 x

Using conversion $x^{2} + y^{2} = r^{2}$ and $x = r cos θ$

\to r^{2} = 2 r cos θ

\to r = 2 cos θ

Double Integrals in Polar Coordinates

Suppose we wish to find the volume of the solid beneath the surface $z = f (x, y)$ and above the region $D$ , where $D$ is described in polar coordinates. We seek:

\int \int_{D} f (x, y) d A = \int \int_{D} f (r cos θ, r sin θ) d A

where we have made the substitution $x = r cos θ$ , $y = r sin θ$ , and $d A$ represents the area element in polar coordinates. To determine the area element, we must understand what it means to integrate over a polar region. The general polar region given by $D$ , where

D = {(r, θ) : a \leq r \leq b, α \leq θ \leq β}

represents the following sector:

Sketch

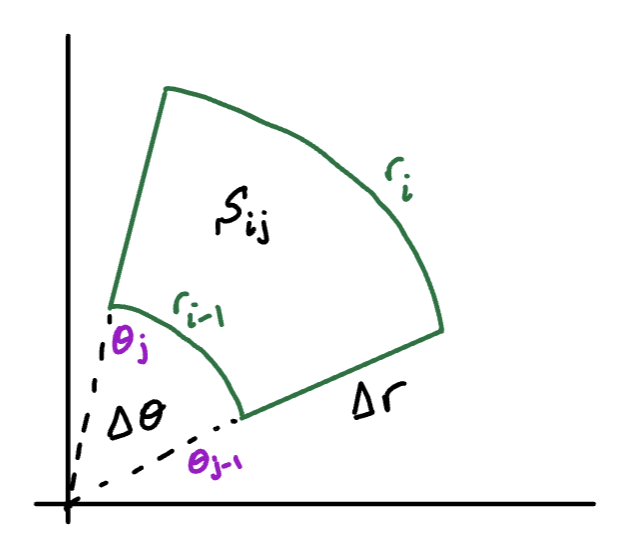
If we divide $[a, b]$ into $m$ sub-intervals of width $Δ r = \frac{b - a}{m}$ , and $[α, β]$ into n sub-intervals of width $Δ θ = (β - α) ∣ n$ , we obtain $m \times n$ sub-sectors (see the right-side of the above figure).

Let’s determine the area of a sub-sector:

Sketch

For very small $Δ r$ and $Δ θ$ , the sub sector is nearly a rectangle with height $Δ r$ and width equal to the arc length of one side of the sector. If we choose the “long” side, the arc length is $r_{i} Δ θ$

Therefore:

A re a o f S_{ij} = Δ A = Δ r \cdot r_{i} Δ θ = r i_{i} Δ r Δ θ

When we take the $lim_{m, n \to \infty}$ , the polar area element is:

Polar Area Element

$d A = r d r d θ$

Using this expression, we obtain the following:

Important

If $f$ is continuous on a “polar rectangle” $D$ given by $a \leq r \leq b$ , $α \leq θ \leq β$ , then:

$\int \int_{D} f (x, y) d A = \int_{α}^{β} \int_{a}^{b} f (r cos θ, r sin θ) r d r d θ$

Observe the extra factor of r that must be included!

Examples

Example

Evaluate:

$\int \int_{D} (3 x + 4 y^{2}) d A$

where $D$ is the semi-annulus shown at the beggining, $1 \leq x^{2} + y^{2} \leq 4$ .

Solution

We integrate in polar coordinates with respect to $r$ and $θ$ , so we must determine bounds on $r$ and $θ$ . From the figure at the beggining, $D$ can be described as:

D = {(r, θ) : 1 \leq r \leq 2, 0 \leq θ \leq π}

We make the substitutions $x = r cos θ$ , $y = sin θ$ , $d A = r d r d θ$ , into the integrand to obtain:

\int \int_{D} (3 x + 4 y^{2}) d A = \int_{0}^{π} \int_{1}^{2} (3 r cos θ + 4 r^{2} sin^{2} θ) r d r d θ

= \int_{0}^{π} \int_{1}^{2} 3 r^{2} cos θ + 4 r^{3} sin^{2} θ d r d θ

Carry out the integration:

I_{1} : \int_{1}^{2} 3 r^{2} cos θ + 4 r^{3} sin^{2} θ d r = r^{3} cos θ + r^{4} sin^{2} θ_{1}^{2}

= 8 cos θ + 16 sin^{2} θ - cos θ - sin^{2} θ

= 7 cos θ + 15 sin^{2} θ

I_{2} : \int_{0}^{π} 7 cos θ + 15 sin^{2} θ d θ = \int_{0}^{π} 7 cos θ + \frac{15}{2} (1 - cos 2 θ) d θ

We use the half angle identity:

= 7 sin θ + \frac{15}{2} θ - \frac{15}{4} sin (2 θ)_{0}^{π} = \frac{15 π}{2}

Remark

The half angle identities will be useful for these problems:

$cos^{2} θ = \frac{1 + c o s ( 2 θ )}{2}, sin^{2} θ = \frac{1 - c o s ( 2 θ )}{2}$

The Gaussian Integral

We will now prove the famous result:

\int_{- \infty}^{\infty} e^{- x^{2}} d x = π

This is the so-called Gaussian Integral

Proof

Observe that:

$\int_{- \infty}^{\infty} \int_{- \infty}^{\infty} e^{- (x^{2} + y^{2})} d x d y = \int_{- \infty}^{\infty} e^{- x^{2}} d x \cdot \int_{- \infty}^{\infty} e^{- y^{2}} d y$

(*)

because we can write the first integrand as a product of two functions independent of each other. The improper integrals on the right-hand side have the same value, so (*) says:

\int_{- \infty}^{\infty} \int_{- \infty}^{\infty} e^{- (x^{2} + y^{2})} d x d y = (\int_{- \infty}^{\infty} e^{- x^{2}} d x)^{2}

(**)

We will compute. the double integral on the left-hand side with polar coordinates.

The integration region is $- \infty < x < \infty$ , $- \infty < y < \infty$ , i.e., the entire xy-plane. In polar coordinates, we can describe the xy-plane by $0 \leq θ \leq 2 π$ , $0 \leq r \leq \infty$ . The Double Integral becomes:

\int_{- \infty}^{\infty} \int_{- \infty}^{\infty} e^{- (x^{2} + y^{2})} d x d y = \int_{0}^{2 π} \int_{0}^{\infty} e^{- r^{2}} \cdot r d r d θ

Solving with I1 and I2

$I_{1} :$ This is an improper integral of the first kind:

\int_{0}^{\infty} r e^{- r^{2}} d r = t \to \infty lim \int_{0}^{t} r e^{- r^{2}} d r

Using U-sub: $u = r^{2}, d u = 2 r d r, r \to \infty$ means $t \to \infty$

= t \to \infty lim \int_{0}^{t} \frac{1}{2} e^{- u} d u

= t \to \infty lim - \frac{1}{2} e^{- u}_{0}^{t}

= t \to \infty lim - \frac{1}{2} e^{- t} + \frac{1}{2}

= 0 + \frac{1}{2} = \frac{1}{2}

Now for I2

I_{2} : \int_{0}^{2 π} \frac{1}{2} d θ = π

Therefore:

\int_{- \infty}^{\infty} \int_{- \infty}^{\infty} e^{- (x^{2} + y^{2})} d x d y = π

Substituting into (**), We get:

(\int_{- \infty}^{\infty} e^{- x^{2}} d x)^{2} = π

Taking the square root yields the result.

Remark

We know it’s the positive square root because $e^{- x^{2}}$ is a positive function.

Graph View

15.3 - Double Integrals in Polar Coordinates

MatPlotLib Example

Polar Coordinate Examples

Double Integrals in Polar Coordinates

Examples

The Gaussian Integral

Solving with I1 and I2

Table of Contents

Backlinks

Explore

Explore