Batch Normalization

What is Batch Normalization?

Batch Normalization (BN) is a technique used in deep learning to improve the training speed and performance of neural networks by normalizing the inputs to each layer. This helps mitigate the problem of internal covariate shift, where the distribution of inputs to a layer changes during training, making convergence slower and more challenging.

Why Use Batch Normalization?

• Faster Training: By normalizing the inputs to each layer, BN helps stabilize and speed up the learning process.
• Higher Learning Rates: It allows the use of higher learning rates, which can further accelerate the convergence.
• Regularization Effect: BN has a slight regularization effect, reducing the need for dropout or other forms of regularization.
• Reduces Sensitivity to Initialization: Neural networks become less sensitive to poor initialization since the normalization keeps activations in check.

How It Works

BN normalizes the output of a layer by adjusting and scaling the activations based on the statistics of the mini-batch. The main steps include:

1. Calculate Mean: Compute the mean of the mini-batch for each feature.
2. Calculate Variance: Compute the variance of the mini-batch for each feature.
3. Normalize: Subtract the mean from the input and divide by the variance to standardize the values.
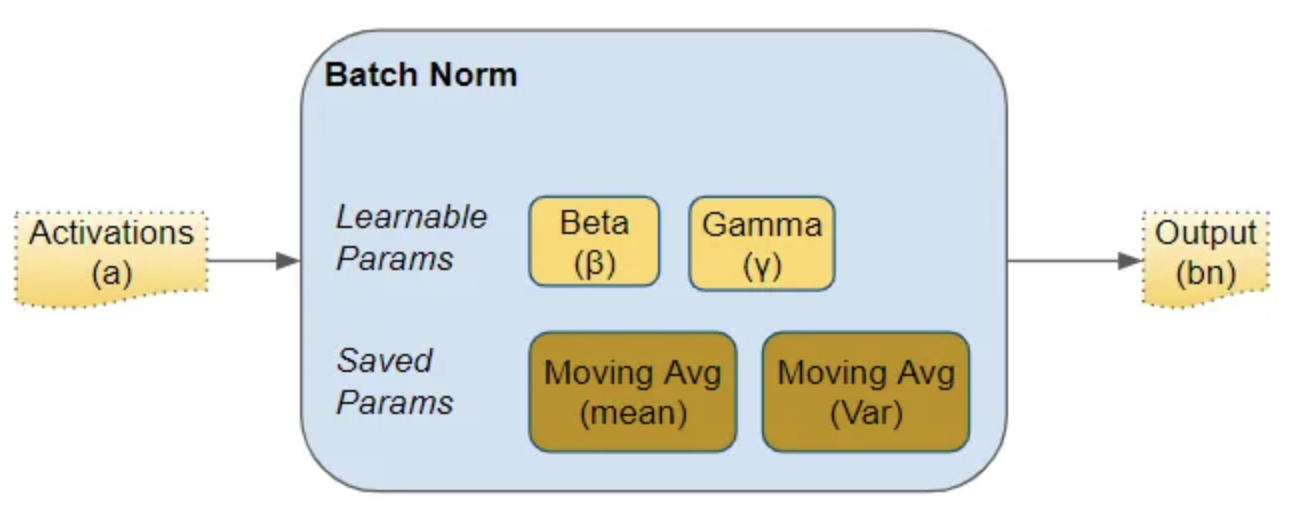
4. Scale and Shift: After normalization, scale the normalized output by multiplying by a trainable parameter, γ (gamma), and shifting it by another parameter, β (beta).

The formula for Batch Normalization:

$${\hat{x}}^{(i)}=\frac{x^{(i)}-{\mu }_B}{\sqrt{{\sigma }_B^2+ϵ}}$$

where:

• $x^{(i)}$ is the input for the $i_{th}$ neuron in the layer.
• ( \mu_B ) is the mean of the mini-batch.
• ( \sigma_B^2 ) is the variance of the mini-batch.
• ( \epsilon ) is a small constant added for numerical stability.
• ( \hat{x}^{(i)} ) is the normalized value.
• γ (gamma) and β (beta) are trainable parameters to scale and shift the normalized output.

Advantages

• Improves Convergence: Batch Normalization accelerates the convergence of training, allowing the use of higher learning rates.
• Works with Different Models: Can be applied to fully connected layers, convolutional layers, and even recurrent neural networks.
• Regularization: BN adds a slight regularization effect, making models less prone to overfitting, although this does not replace other regularization techniques.

Limitations

• Batch Dependence: BN works best with large batch sizes. Small batches may lead to inaccurate statistics (mean and variance).
• Complexity: Adds computational overhead since it requires maintaining additional moving averages of batch statistics during training.
• Training and Inference Difference: During inference, BN uses running averages of the mean and variance computed during training, which may lead to performance drops if batch statistics are not well-calibrated.

Code Example (PyTorch)

import torch
import torch.nn as nn
 
class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.fc1 = nn.Linear(784, 256)
        self.bn1 = nn.BatchNorm1d(256)
        self.fc2 = nn.Linear(256, 10)
    
    def forward(self, x):
        x = self.fc1(x)
        x = self.bn1(x)  # Apply Batch Norm after the first layer
        x = torch.relu(x)
        x = self.fc2(x)
        return x
 
model = Net()