14.6 - Directional Derivatives

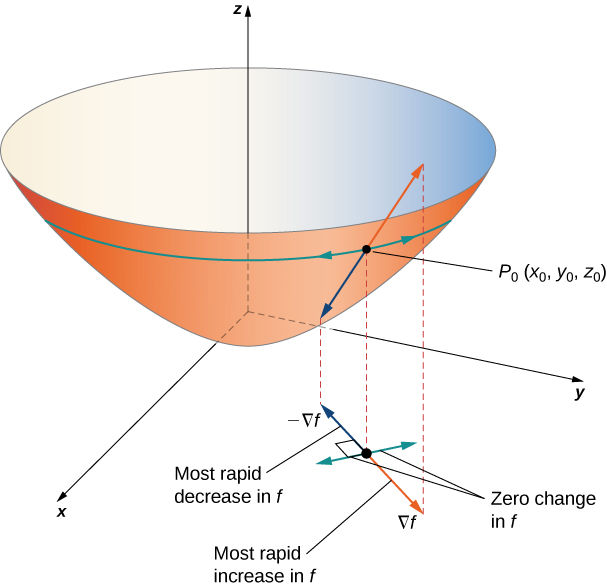
Directional Derivatives serve to help us understand how a function changes in a particular direction. The gradient is a vector that points in the direction of the steepest increase of a function. The gradient is a generalization of the derivative to functions of multiple variables.

---

Abstract

example graph

import micropip
await micropip.install("matplotlib")
await micropip.install("numpy")
 
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
 
# Create figure and 3D axis
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
 
# Define the grid for the plane
x = np.linspace(-5, 5, 30)
y = np.linspace(-5, 5, 30)
x, y = np.meshgrid(x, y)
z = 0.5 * x + 0.2 * y  # Equation of a plane: z = 0.5x + 0.2y
 
# Plot the plane
ax.plot_surface(x, y, z, cmap=cm.viridis, alpha=0.6)
 
# Define a point on the plane
point = np.array([2, 1, 0.5 * 2 + 0.2 * 1])  # (x, y, z) = (2, 1, 1.2)
 
# Plot the point
ax.scatter(point[0], point[1], point[2], color='r', s=100)
 
# Define a direction vector
direction = np.array([1, 1, 0.5 * 1 + 0.2 * 1])  # Vector with slope matching the plane
 
# Normalize the direction for plotting an arrow
direction_normalized = direction / np.linalg.norm(direction)
 
# Plot the direction as an arrow from the point
ax.quiver(point[0], point[1], point[2], direction_normalized[0], direction_normalized[1], direction_normalized[2], color='b', length=2, arrow_length_ratio=0.2)
 
# add a projection at the bottom of the graph of where the direction vector is pointing
ax.plot([point[0], point[0] + direction_normalized[0]], [point[1], point[1] + direction_normalized[1]], [0, 0], color='b', linestyle='--')
 
# Set labels
ax.set_xlabel('X axis')
ax.set_ylabel('Y axis')
ax.set_zlabel('Z axis')
ax.set_title('3D Plane with Point and Direction')
 
# Show plot
plt.show()
 

Given $z=f(x,y)$ and the point $z_0=f(x_0,y_0)$ we seek the slope of the tangent line at $z_0$ in the direction of the unit vector $\vec{u}$

We are seeking to find the secant line $m_{secant}$ that passes through the point $(x_0,y_0,z_0)$ and $(x_0+a,y_0+b,z_0+c)$

For this purpose, we will use the abstract equation:

$m_{secant}=\frac{verticalchange}{horizontalchange}$

Where:

• vertical change is the change in z coordinates
• horizontal change is the change in x and y coordinates

Plugging in the imaginary values:

$=\frac{f(x_1,y_1)-f(x_0,y_0)}{|\vec{u}t|}$

Where:

• $x_1=x_0+at$ is the x coordinate of the point on the secant line
• $y_1=y_0+bt$ is the y coordinate of the point on the secant line
• $z_1=z_0+ct$ is the z coordinate of the point on the secant line
• $\vec{u}=<a,b>$ is the direction vector

Putting this all together, we get a graph that looks something like this:

In Layman’s Terms

Essentially, the directional derivative is a measure of how a function changes in a specific direction. The gradient is a vector that points in the direction of the steepest increase of a function. The gradient is a generalization of the derivative to functions of multiple variables.

Proofs

Definition

${\lim }_{t\to 0}\frac{f(x_0+u_{1}t,y_0+u_{2}t)-f(x_0,y_0)}{t}=D_{\vec{u}}f(x_0,y_o)$ Directional Derivative of f at $(x_0,y_0)$ in the direction of $\vec{u}$, where $\vec{u}$ is unit vector $D_{\vec{u}}f(x_0,y_0)=\nabla f(x_0,y_0)\cdot \vec{u}$

Key Formula

Formula

$\nabla f=\partial f\partial x,\partial f\partial y$

This enables us to calculate the directional derivative in an arbitrary direc- tion, by taking the dot product of ∇f with a unit vector, u, in the desired direction.

---

Example

Example

Find the directional derivative of: $f(x,y)=x^2{y}^3-4y$ at the point $(2,-1)$ in the direction of $\vec{v}=⟨2,5⟩$

Lets start by finding the gradient of $f(x,y)$:

Tip

Always normalize the direction vector into a unit vector

$D\_\vec{u}f(2,-1)=\nabla f\cdot \vec{u}=⟨\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}⟩\cdot ⟨\frac{2}{\sqrt{29}},\frac{5}{\sqrt{29}}⟩$

After finding the gradient, we can plug in the values:

$=\frac{4x^2{y}^3-4y}{\sqrt{29}}$

Conclusively, the directional derivative of $f(x,y)$ at the point $(2,-1)$ in the direction of $\vec{v}$ is $\frac{4x^2{y}^3-4y}{\sqrt{29}}$

Conclusion:

The directional derivative of $f(x,y)$ at the point $(2,-1)$ in the direction of $\vec{v}$ is $\frac{4x^2{y}^3-4y}{\sqrt{29}}$

---

Example 2