15.1 - Multiple Integrals

Consider the function $z=f(x,y)$ defined over the closed rectangle

$R=[a,b]\times [c,d]=\{(x,y):a\le x\le b,c\le y\le d\}$

(The “x” in this context is called the Cartesian Product)

---

Graphing and Dividing

Suppose that $z\ge 0$ for all $(x,y)\in \mathbb{R}$

MatPlotLib Graph

Goal

Find the volume of the solid beneath S and above R

We proceed by dividing R into $m\times n$ subrectangles.

Stencil

Subdivision of R with m=5 and n=4

This is called the “Stencil”

$R_{14}$	$R_{24}$	$R_{34}$	$R_{44}$	$R_{54}$
$R_{13}$	$R_{23}$	$R_{33}$	$R_{43}$	$R_{53}$
$R_{12}$	$R_{22}$	$R_{32}$	$R_{42}$	$R_{52}$
$R_{11}$	$R_{21}$	$R_{31}$	$R_{41}$	$R_{51}$

Where a point like $(x_{43},y_{43})$ can sit somewhere in the $R_{43}$ subrectangle

If we choose a sample point $(x_{ij}^{\ast },y_{ij}^{\ast })$ in each subrectangle $R_{ij}$ , we can approximate the volume beneath S and above $R_{ij}$ by the rectangular prism with base $R_{ij}$ and height $f(x_{ij}^{\ast },y_{ij}^{\ast })$.

If we call the area of $R_{ij}$ $\nabla A$, then the volume of the rectangular “box” is

$V=f(x_{ij}^{\ast },y_{ij}^{\ast })\nabla A$

---

Total Volume Approximation

We can approximate the total volume by summing the volumes of all the boxes represented in the stencil.

$Volume=\sum (Allrectangularboxes)$

$Volume={\sum }_{i=1}^m{\sum }_{j=1}^{n}f(x_{ij}^{\ast },y_{ij}^{\ast })\nabla A$

The “double-sum” means

Start at $i=1$, then sum through all the j’s. Then step up to $i=2$ and sum through all the j’s. Repeat through $i=m$. So, for the Stencil, we get

${\sum }_{i=1}^m{\sum }_{j=1}^n{R}_{ij}=R_{11}+R_{12}+R_{13}+R_{14}+\dots$

$=R_{21}+R_{22}+\dots$

$⋮$

$=R\ast 51+R\ast 52+\dots$

Note

We use $R_{ij}$ as a shorthand to illustrate how the double-sum captures all elements in the stencil

Intuitively, the estimation of the true volume will improve as the number of subrectangles increases, and we define

$Volume={\lim }_{m,n\to \infty }{\sum }_{i=1}^m{\sum }_{j=1}^{n}f(x_{ij}^{\ast },y_{ij}^{\ast })\nabla A$

We define the Double Integral as this sum

Definition

${\int }_R\int f(x,y)dA={\lim }_{m,n\to \infty }{\sum }_{i=1}^m{\sum }_{j=1}^{n}f(x_{ij}^{\ast },y_{ij}^{\ast })\nabla A$

Where the Double Rienmann Sum is ${\sum }_{i=1}^m{\sum }_{j=1}^{n}f(x_{ij}^{\ast },y_{ij}^{\ast })\nabla A$

This definition has some symbols we have not seen before, so let’s take a second to learn them.

---

Familiarizing Ourselves With Reading Integration Symbols

• $R$ describes the region of integration
• $dA$ is the area element, meaning the area of the base of each “box” in the sum in the limit $m,n\to \infty$
• So, we think of the double integral as

$Volume=\int \int (Height)(AreaElement)$

The presence of two integral signs indicates the dimension of the integration region.

i.e. $R$ is a 2D-Rectangle

Remark

This particular double integral can be interpreted as “signed volume”

---

Examples

Example

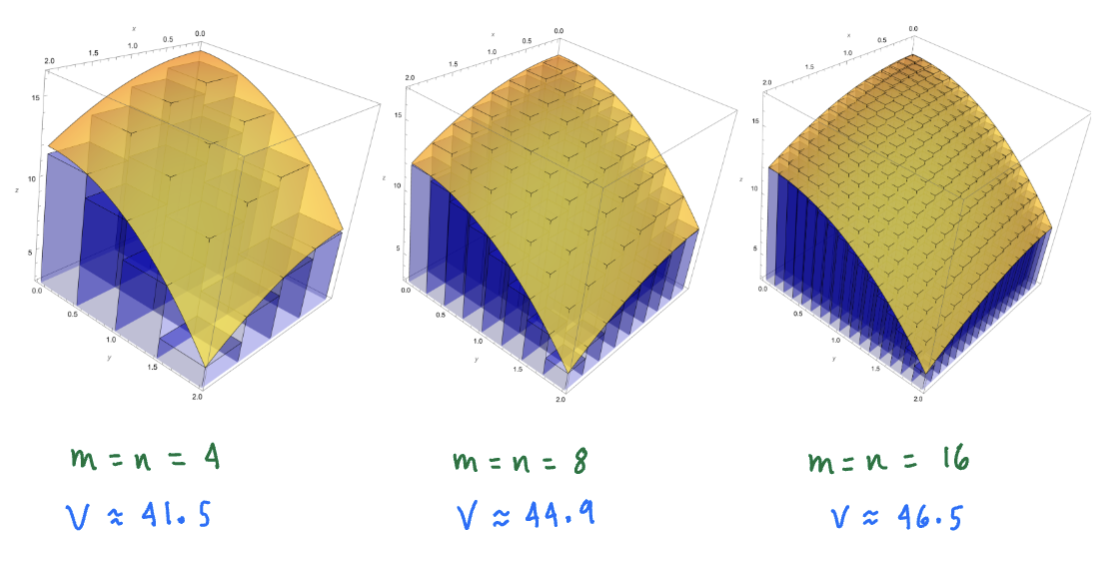
Estimate the volume of the solid that lies above the rectangle

$R=[0,2]\times [0,2]$

and below the elliptic parabaloid

$z=16-x^2-2y^2$

Solution

The idea here is to approximate

$\int {\int }_R(16-x^2-2y^2)dA$

We can do this by evalutating the double-Rienmann sum for increasing values of $m$ and $n$. This is a brutal calculation by hand, so we will use Mathematica to calculate and illustrate the sum.

Sketch

As we can see, the approximation to the true volume improves as the number of boxes increases. Later, we will be able to show that the true volume is 48(fairly close to the approximation using $16\times 16=256$ boxes)

---

Double Integration by Geometry

If we interpret the double integral as a volume, we can somtimes evalutate these integrals using geometry.

Example

If:

$R=[-1,1]\times [-2,2]$

Evalutate: