16.1 - Vector Fields

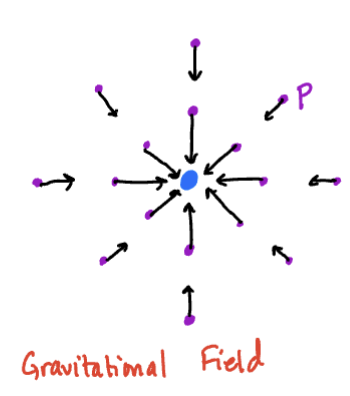
A vector field is a function that associates a point with a vector. An example is Earth’s gravitational field:

Sketch

The Earth exerts an attractive force on a point-mass located anywhere inthe universe. At every point $P$, wer draw a vector pointing in the direction of the attractive force with length equal to the magnitude of the force.

(according to Newton, the magnitude of the force is inversely proportional to the distance from the point to the Earth.)

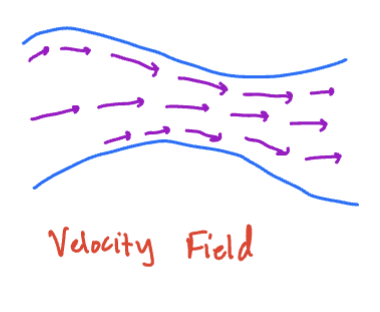
Vector fields are convenient for problems involving Flow. Consider the problem of water flowing through a stream:

Sketch

At every point in the stream, we can assign a vector whivh tells use the direction the water is moving. The magnitude of the vector tells us the velocity of the water at that point.

---

Notation

The vector field $\vec{F}$ has the notation:

$$\vec{F}(x,y)=P(x,y)\vec{i}+Q(x,y)\vec{i}=⟨(x,y),Q(x,y)⟩$$

Where $P$ and $Q$ are scalar functions.

Example

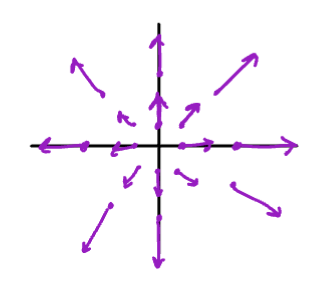
Sketch the vector field $\vec{F}=x\vec{i}+y\vec{j}=⟨x,y⟩$

Solution

When we input the point $(x,y)$, $\vec{F}$ outputs the vector $⟨x,y⟩$. Meaning: at the point $(x,y)$, we sketch the position vector $⟨x,y⟩$.

Sketch

Remark

The initial points of the vector are drawn from the point $(x,y)$; e.g. at $(1,1)$ we draw the vector $⟨1,1⟩$

Observe

The vectors in this field “diverge” from a source, such as the velocity of air in an explosion

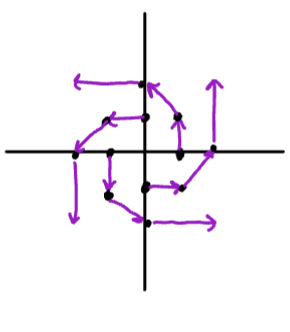
Sketch the field \vec{F} = -y \vec{i}+x \vec{j} =\langle-y,x\rangle

Sketch

This sketch comes from plotting a few example vectors until we notice that pattern:

$$\begin{array}{c}@(1,0):\vec{F}=⟨0,1⟩\\ @(0,1):\vec{F}=⟨-1,0⟩\\ @(-1,0):\vec{F}=⟨0,-1⟩\\ @(0,-1):\vec{F}=⟨1,0⟩\\ @(1,1):\vec{F}=⟨-1,1⟩\\ @(-1,1):\vec{F}=⟨-1,-1⟩\end{array}$$

Observe:

The vector field “rotates”, such as air in a tornado

---

Vector Fields in Mathematica

Sketching vector fields by hand is very tedious, especially if the vector field is 3-dimensional, e.g. $\vec{F}=y\vec{i}+z\vec{j}+x\vec{k}$.

MUST SEE: the Mathematica file called “vector fields” for a demo of the VectorPlot and VectorPlot3D commands

EXTRA: we can also use MatPlotLib to do the same

note: my code interpreter does not allow for a dynamic canvas just yet, so if you want the full render run this code on your own machine.

Python

import numpy as np import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D # Define the grid range and resolution x = np.linspace(-2, 2, 10) y = np.linspace(-2, 2, 10) z = np.linspace(-2, 2, 10) X, Y, Z = np.meshgrid(x, y, z) # Define the vector field components U = Y # i-component (y-component of the field) V = Z # j-component (z-component of the field) W = X # k-component (x-component of the field) # Plot the vector field fig = plt.figure(figsize=(10, 8)) ax = fig.add_subplot(111, projection='3d') # Create the quiver plot ax.quiver(X, Y, Z, U, V, W, length=0.2, normalize=True, color='b', arrow_length_ratio=0.5) # Set plot limits and labels ax.set_xlim([-2, 2]) ax.set_ylim([-2, 2]) ax.set_zlim([-2, 2]) ax.set_xlabel('X') ax.set_ylabel('Y') ax.set_zlabel('Z') ax.set_title(r'3D Vector Field $\vec{F} = y \vec{i} + z \vec{j} + x \vec{k}$') plt.show()

Output

---

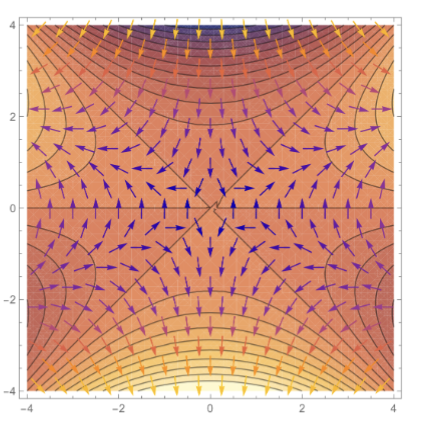
Gradient Vector Fields

Recall that $\nabla f=⟨f_x,f_y,f_z⟩=f_x\vec{i}+f_y\vec{j}+f_z\vec{k}$. Thus, the gradient vector is really a vector field.

Graph

Example

The gradient vector field for $f(x,y)=x^{2}y-y^3$, superimposed on the contour map. As we would expect, the gradient vectors are perpendicular to the contours.

---

Conservative Vector Fields

We say $\vec{F}$ is a conservative vector field if $\vec{F}=\nabla f$ for some scalar function $f$. In this context, $f$ is called a potential function for $\vec{F}$. Conservative vector fields will be important to us soon…