Overview
In a binary search tree (BST), nodes are arranged such that:
- The left child of a node contains a value smaller than the node.
- The right child of a node contains a value greater than the node.
There are four common tree traversal methods and two important search strategies:
- In-order Traversal
- Pre-order Traversal
- Post-order Traversal
- Level-order Traversal
- Breadth-First Search (BFS)
- Depth-First Search (DFS)
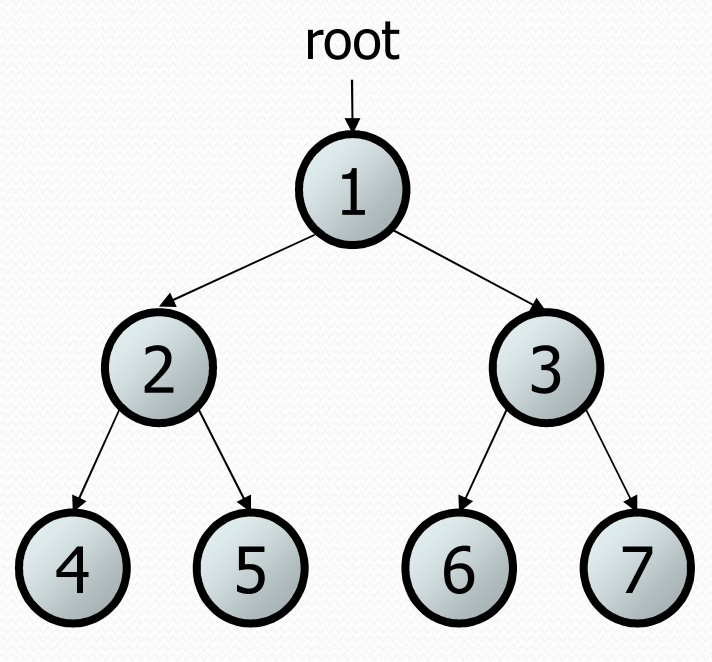
Example Tree
We will be using this tree to illustrate the different strategies you can use to navigate a BST.
1. In-order Traversal
In-order traversal visits nodes in ascending order (for a BST).
Algorithm:
- Traverse the left subtree.
- Visit the root.
- Traverse the right subtree.
Example for the given tree:
- Traverse left subtree of 1 → Traverse left subtree of 2 → Visit 4 → Visit 2 → Visit 5 → Visit 1 → Traverse right subtree of 1 → Visit 6 → Visit 3 → Visit 7
In-order traversal result: 4, 2, 5, 1, 6, 3, 7
Implementation:
void inOrder(Node* root) {
if (root == nullptr) return;
inOrder(root->left);
std::cout << root->data << " ";
inOrder(root->right);
}2. Pre-order Traversal
Pre-order traversal visits the root before its subtrees.
Algorithm:
- Visit the root.
- Traverse the left subtree.
- Traverse the right subtree.
Example for the given tree:
- Visit 1 → Traverse left subtree of 1 → Visit 2 → Visit 4 → Visit 5 → Traverse right subtree of 1 → Visit 3 → Visit 6 → Visit 7
Pre-order traversal result: 1, 2, 4, 5, 3, 6, 7
Implementation:
void preOrder(Node* root) {
if (root == nullptr) return;
std::cout << root->data << " ";
preOrder(root->left);
preOrder(root->right);
}3. Post-order Traversal
Post-order traversal visits the root after its subtrees.
Algorithm:
- Traverse the left subtree.
- Traverse the right subtree.
- Visit the root.
Example for the given tree:
- Traverse left subtree of 1 → Traverse left subtree of 2 → Visit 4 → Visit 5 → Visit 2 → Traverse right subtree of 1 → Visit 6 → Visit 7 → Visit 3 → Visit 1
Post-order traversal result: 4, 5, 2, 6, 7, 3, 1
Implementation:
void postOrder(Node* root) {
if (root == nullptr) return;
postOrder(root->left);
postOrder(root->right);
std::cout << root->data << " ";
}4. Level-order Traversal
Level-order traversal visits nodes level by level.
Algorithm:
- Visit each level of the tree starting from the root.
- Traverse left to right within each level.
Example for the given tree:
- Visit level 1: Visit 1 → Visit level 2: Visit 2, 3 → Visit level 3: Visit 4, 5, 6, 7
Level-order traversal result: 1, 2, 3, 4, 5, 6, 7
Implementation:
void levelOrder(Node* root) {
if (root == nullptr) return;
std::queue<Node*> q;
q.push(root);
while (!q.empty()) {
Node* current = q.front();
q.pop();
std::cout << current->data << " ";
if (current->left != nullptr) q.push(current->left);
if (current->right != nullptr) q.push(current->right);
}
}5. Breadth-First Search (BFS)
Breadth-First Search explores the tree level by level, starting at the root.
Example for the given tree:
- Start at root 1 → Visit 2, 3 → Visit 4, 5, 6, 7
BFS result: 1, 2, 3, 4, 5, 6, 7
Implementation:
bool BFS(Node* root, int target) {
if (root == nullptr) return false;
std::queue<Node*> q;
q.push(root);
while (!q.empty()) {
Node* current = q.front();
q.pop();
if (current->data == target) return true;
if (current->left != nullptr) q.push(current->left);
if (current->right != nullptr) q.push(current->right);
}
return false;
}6. Depth-First Search (DFS)
Depth-First Search explores the tree as deep as possible before backtracking.
DFS - Pre-order example for the given tree:
- Start at root 1 → Visit 2 → Visit 4 → Visit 5 → Visit 3 → Visit 6 → Visit 7
DFS result (Pre-order): 1, 2, 4, 5, 3, 6, 7
Implementation:
bool DFS(Node* root, int target) {
if (root == nullptr) return false;
if (root->data == target) return true;
if (target < root->data) return DFS(root->left, target);
return DFS(root->right, target);
}Inserting Elements into an Empty Binary Search Tree
When inserting elements into an empty BST:
- Recursively place a node into the correct position, adhering to the BST property.
Example insertion sequence:
- To insert the sequence
1, 2, 3, 4, 5, 6, 7into an empty BST:- Start with
1as root. - Insert
2to the right of1(since 2 > 1). - Insert
3to the right of2(since 3 > 2). - Continue similarly for the rest.
- Start with
Implementation:
Node* insert(Node* root, int data) {
if (root == nullptr) {
root = new Node(data);
} else if (data < root->data) {
root->left = insert(root->left, data);
} else {
root->right = insert(root->right, data);
}
return root;
}Summary
Traversals of a BST allow for different ways of visiting and processing nodes. Understanding them is crucial for manipulating and analyzing trees efficiently. BFS and DFS provide powerful ways to search for specific nodes.
- In-order: Left, Root, Right (sorted output for BST).
- Pre-order: Root, Left, Right (copying structure, prefix expressions).
- Post-order: Left, Right, Root (deleting or evaluating postfix expressions).
- Level-order: Breadth-first search (top-down level-wise traversal).
- BFS: Searches the tree level by level.
- DFS: Searches the tree as deeply as possible before backtracking.