In the previous lecture, we examined , where was a rectangular region in the xy-plane. Now we examine the more general case:
Where is a region of any shape in the xy-plane.
note: the symbol used in class looks a little different, but unfortunately there is not LaTeX equivelant
Abstract
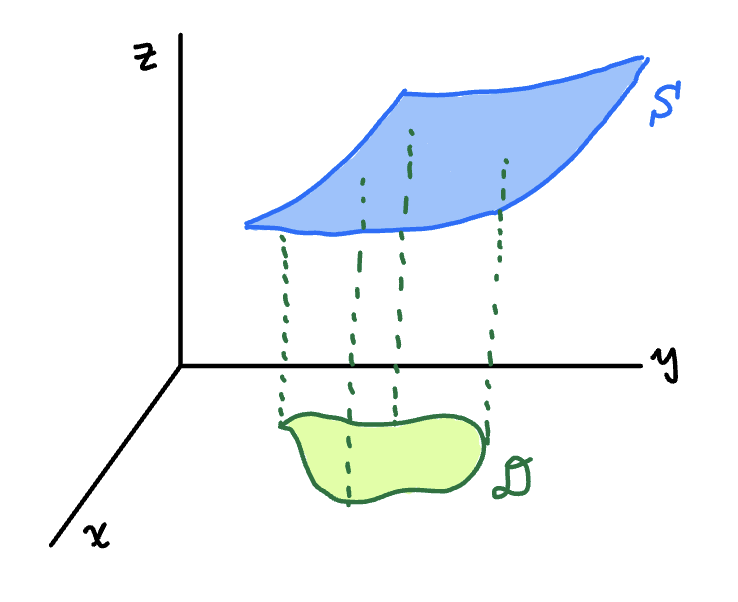
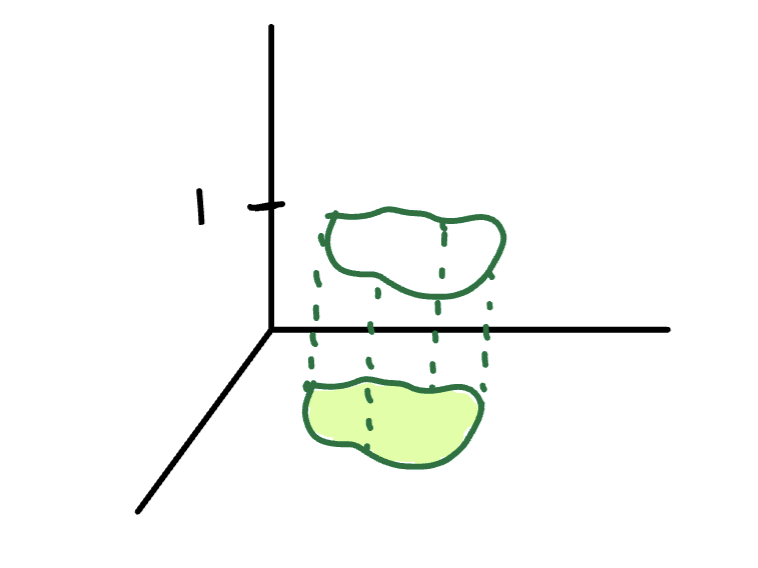
Suppose we have a graph that looks like the following:
Sketch
can be interpreted as the volume of the solid below the surface S and above the region
Simple Regions
We will examine the special case where is a simple region. Two types of simple regions are vertically simple (called Type 1) and Horizontally Simple (called Type 2)
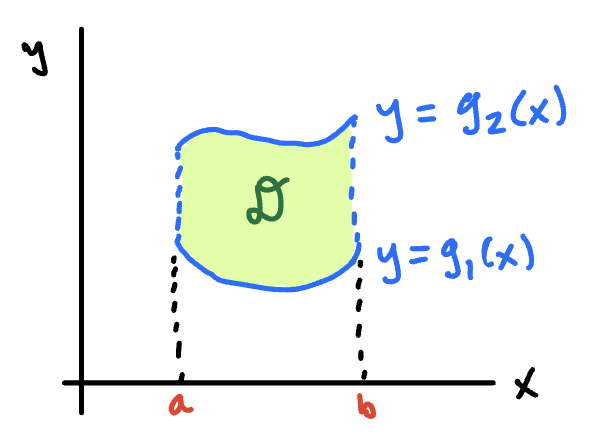
Type 1 Region
Sketch
lies completely between the continuous functions and
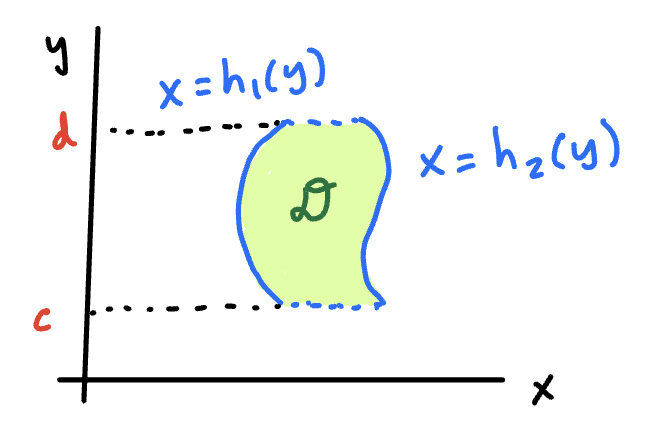
Type 2 Region
Sketch
lies completely between the continuous functions and
Remark
We have dealt with simple regions before; in Calc. 1, we found the area of simple regions in “Area Between Curves” type problems.
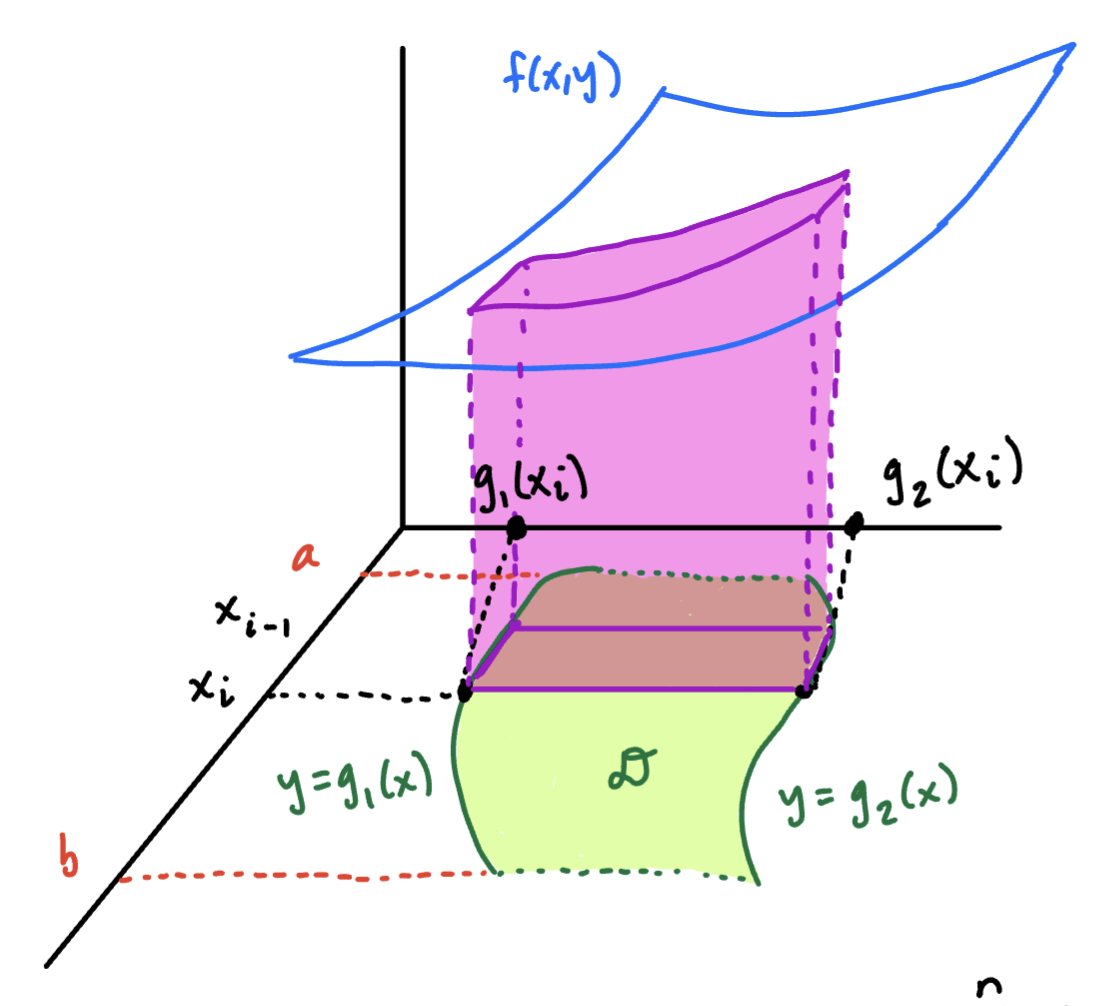
To find a double integral over a simple region, we follow an approach similar to the proof of Fubini’s Theorem. Let be defined of the Type 1 region
Sketch
The idea is to divide the interval into subintervals of width:
then add up the volume of the n Slabs:
The volume of “Slab i” is the width times the area of the face, which is the 2D-integral
Note
Note the limits of integration on the y-axis
The double integral is therefore approximated by:
Taking the limit , we get the following result:
Result
If is continuous on the Type 1 region
then:
A similar argument for Type 2 regions yields:
Result
If is continuous on the Type 2 region
then:
Remarks
- Note how the order of integration is different in each case. In both cases, we integrate the variable whose integration limits can be written in terms of the other variable first.
- DO NOT “blindly” swap the order of integration. That only works for rectangular regions. We can change the order of integration, but it will involve finding new integration limits.
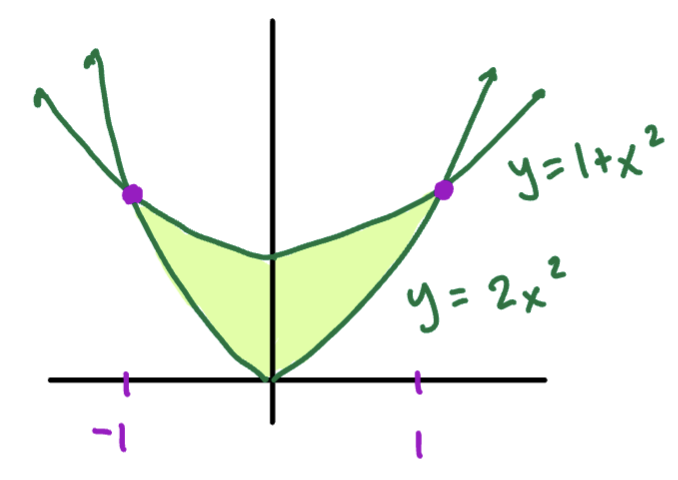
Example
Problem
Evaluate:
Where is the region bounded by the parabolas:
Solution
We should always start by sketching the region .
Sketch
We can see that is Type 1:
The double integral is therefore:
Set-up for Type 1 region
Integrate with respect to y
Integrate with respect to x
Final Answer
Remarks
- This example illustrates the procedure for when we integrate first with respect to
yand then with respect tox. We “integrate out the y” to obtain an integrand entirely in terms ofx, which we evaluate to get a constant. - Setting up the double integral is the important part. We can use Mathematica to handle the actual integration.
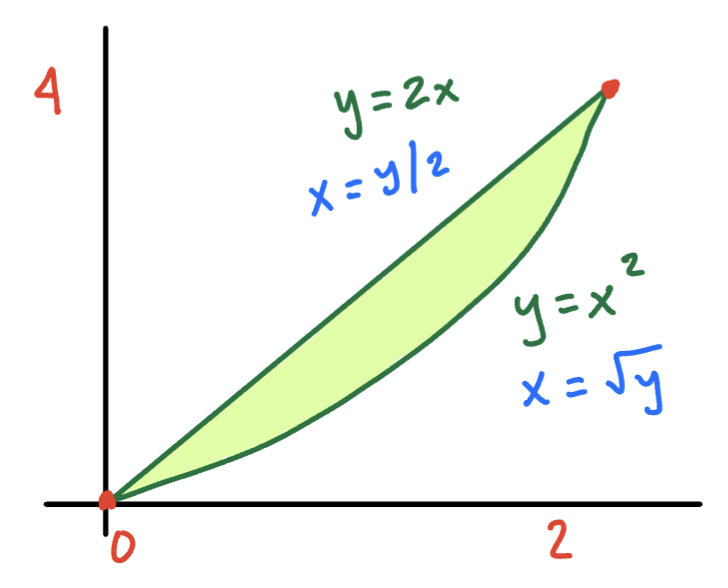
Example
Example
Find the volume of the solid that lies under the paraboloid and above the region in the xy-plane, bounded by the line and
Solution
Sketch the region
Sketch
- As a type 1 region:
- ,
- As a type 2 region:
- ,
We can set up the integral two ways:
Type 1:
Type 2:
Pick whichever integral is easier to find
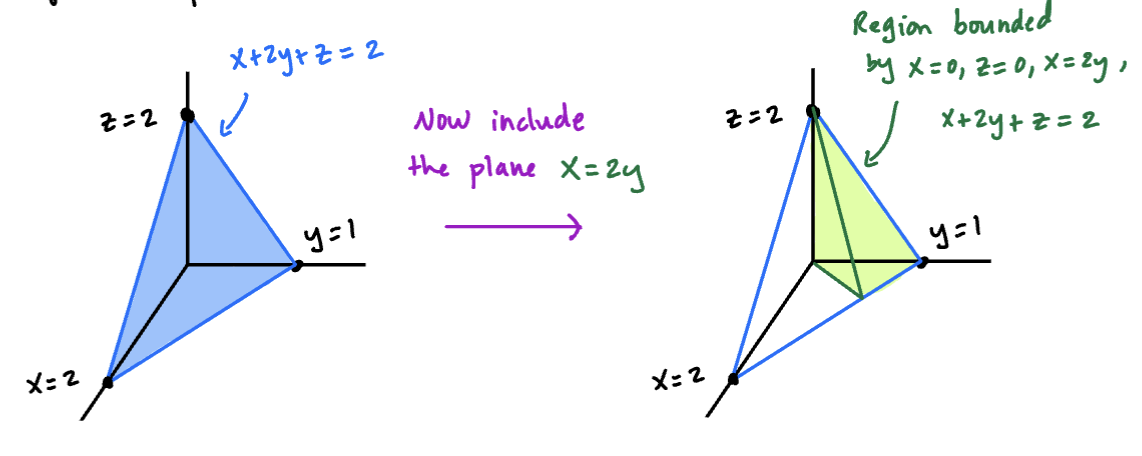
Example
Example
Find hte volume of the tetrahedron bounded by the planes:
Solution
Sometimes, we have to sketch the solid in order to determine the region of integration. Let’s start by sketching the part of the plane in the first octant:
Sketch
Now sketch the integration region in the xy-plane:
Sketch
is the point of intersection of the two lines.
As a Type 1 region,
(we got the bounds on y because )
The volume of the tetrahedron is the volume above and below the plane , which we can express as .
The double integral is:
Changing the order of Integration
We will now examine how to handle changing the order of integration over non-rectangular region of integration.
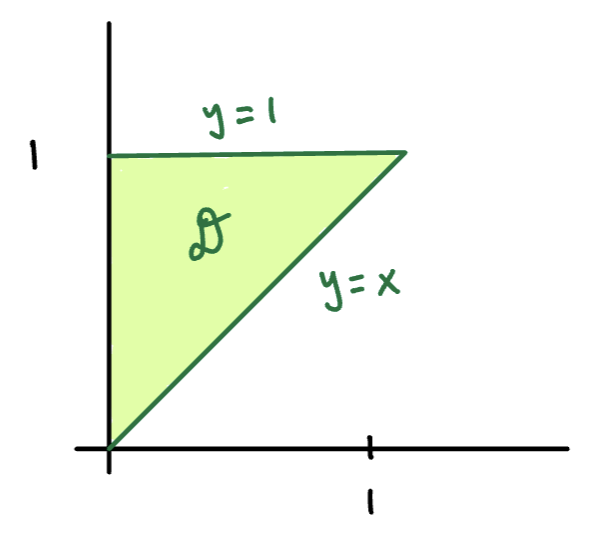
Example
Evaluate:
Solution
This integral calls for a different order because we cant integrate with respect to y ( this is a Fresnel Integral)
We can work backwards to find limits of integration for the order . By reading the original integral, we see that is the region where “runs” from to , and “runs” from to
Sketch
Integration Region ( type 1):
Equivalently (type 2):
From the Sketch, we see that is treated as a Type 1 region in the original integral. If we treat as a Type 2 region, the integral becomes:
This changed the order of integration and gave us something we are able to integrate.
Finding Area Using Double Integrals
Observe that:
Where means the area of region . This is because the integral represents the volume of the solid below the plane and above the region , which is merely a cylinder:
Sketch
Where:
Remark
In 2D, gives the length of the interval of integration. So,
Triple Integral Coming soon…