15.7 - Triple Integrals in Cylindrical Coordinates

Cylinderical Coordinates are the three-dimensional analogue of polar coordinates. They are useful for describing regions with rotational symmetry.

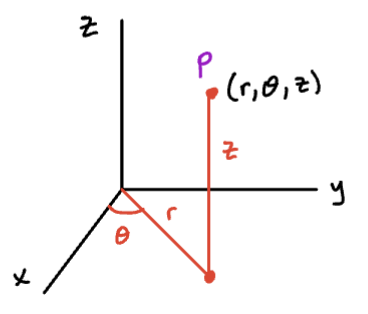
In cylindrical coordinates, the point P$(r,\theta ,z)$ means the following:

• $r$ and $\theta$ are the polar coordinates of the projection of P onto the xy-plane.
• $z$ is the distance from P to the xy-plane

Sketch

The relationship between cylindrical and Cartesian coordinates is:

$$x=r\cos \theta ,y=r\sin \theta ,z=z$$

This comes from the fact that the x- and y-coordinates of a point in cylindrical coordinates can be expressed in polar. We also have:

Key Formula

$$x^2+y^2=r^2$$

---

Applications

Example

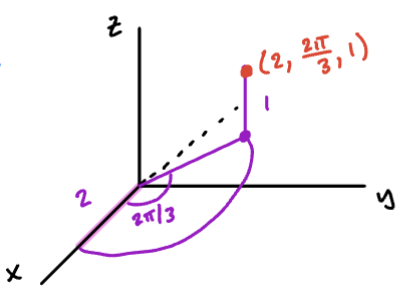
Plot the point with cylinderical coordinates $\left(2,\frac{2\pi }{3},1\right)$ and convert to rectangular coordinates.

Solution

To plot $(r,\theta ,z)=(2,\frac{2\pi }{3},1)$, plot $(r,\theta )=(2,\frac{2\pi }{3})$ in polar coordinates in the xy-plane, then move vertically $z=1$ unit.

Sketch

To find the rectangular coordinates, use the above formulae:

$$X=r\cos \theta =2\cos \left(\frac{2\pi }{3}\right)=2\left(-\frac{1}{2}\right)=1$$ $$Y=r\sin \theta =2\sin \left(\frac{2\pi }{3}\right)=2\left(\frac{\sqrt{3}}{2}\right)=\sqrt{3}$$ $$Z=z=z$$

This yields a rectangular result:

$$(-1,\sqrt{3},1)$$

Example

Identify the surface $r=c$

Solution

Square both sides and use the key formula:

$r=c\to r^2=c^2\to x^2+y^2=c^2$

This is a cylinder of radius C

---

Triple Integrals in Cylinderical Coordinates

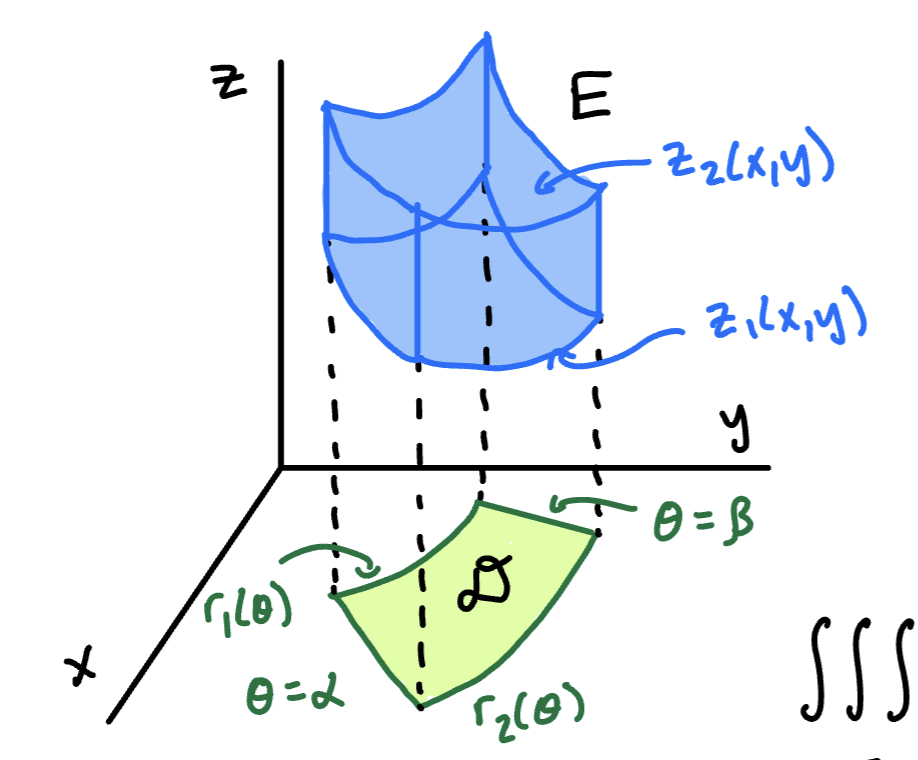
Suppose $E$ is a Type 1 region whose projection $\mathcal{D}$ onto the xy-plane can be described conveniently on polar coordinates.

$E$ is a Type 1 region, so it’s bounded between the surfaces $z_1(x,y)$ and $z_2(x,y)$. We can therefore write:

$$\int \int {\int }_{E}f(x,y,z)dV=\int {\int }_{\mathcal{D}}{\int }_{z_1(x,y)}^{z_2(x,y)}f(x,y,z)dzdA$$

Sketch

But we know how to integrate over $\mathcal{D}$ in polar coordinates:

$$\int {\int }_{\mathcal{D}}{\int }_{z_1(x,y)}^{z_2(x,y)}f(x,y,z)dA={\int }_{\alpha }^{\beta }{\int }_{r_1(\theta )}^{r_2(\theta )}{\int }_{z_1(x,y)}^{z_2(x,y)}f(x,y,z)rdzdrd\theta$$

Converting x and y to polar coordinates, we have the result:

$$\int \int {\int }_{E}f(x,y,z)dV={\int }_{\alpha }^{\beta }{\int }_{r_1(\theta )}^{r_2(\theta )}{\int }_{z_1(r\cos \theta ,r\sin \theta )}^{z_2(r\cos \theta ,r\sin \theta )}f(r\cos \theta ,r\sin \theta ,z)rdzdrd\theta$$

Remarks

1. To integrate in cylindrical coordinates, we convert x and y to polar and leave z alone. We “run” z from the bottom surface to the top surface, then integrate over $r$ and $\theta$ as we did with double integrals in polar coordinates.

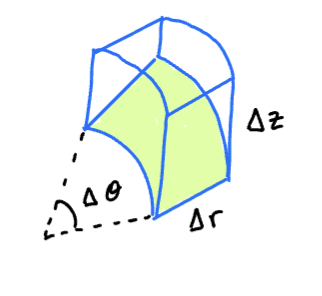
2. The expression $rdzdrd\theta$ represents the volume element in cyldindrical coordinates. The volume of the volume element is the area of the base times the height. But the base is the polar area element, whichi has area $r\Delta r\Delta \theta$, and the height is $\Delta z$, so we get:

Sketch

$$Volume-(r\Delta r\Delta \theta )(\Delta z)=r\Delta z\Delta r\Delta \theta$$ $$\to rdzdrd\theta$$

in the limiting process of the integral.

---

Example

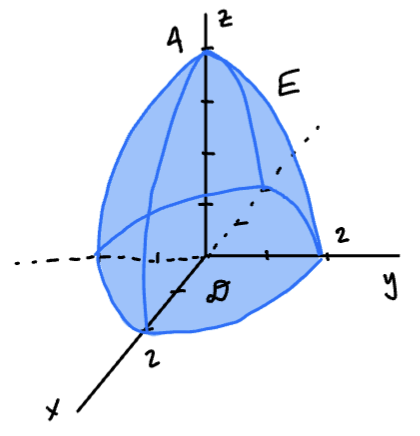
Evaluate:

$$\int \int {\int }_E{x}^{2}dV$$

where $E$ is the solid that lies under the paraboloid $z=4-x^2-y^2$ and above the xy-plane.

Solution

Sketching reveals how to handle this problem:

Sketch

Observe that the projection of the surface onto the xy-plane is the disk $x^2+y^2\le 4$. Algebraically, we can use this by setting $z=0$ in the equation $z=4-x^2-y^2$.

1. Obtain limits on z in cylindrical coordinates

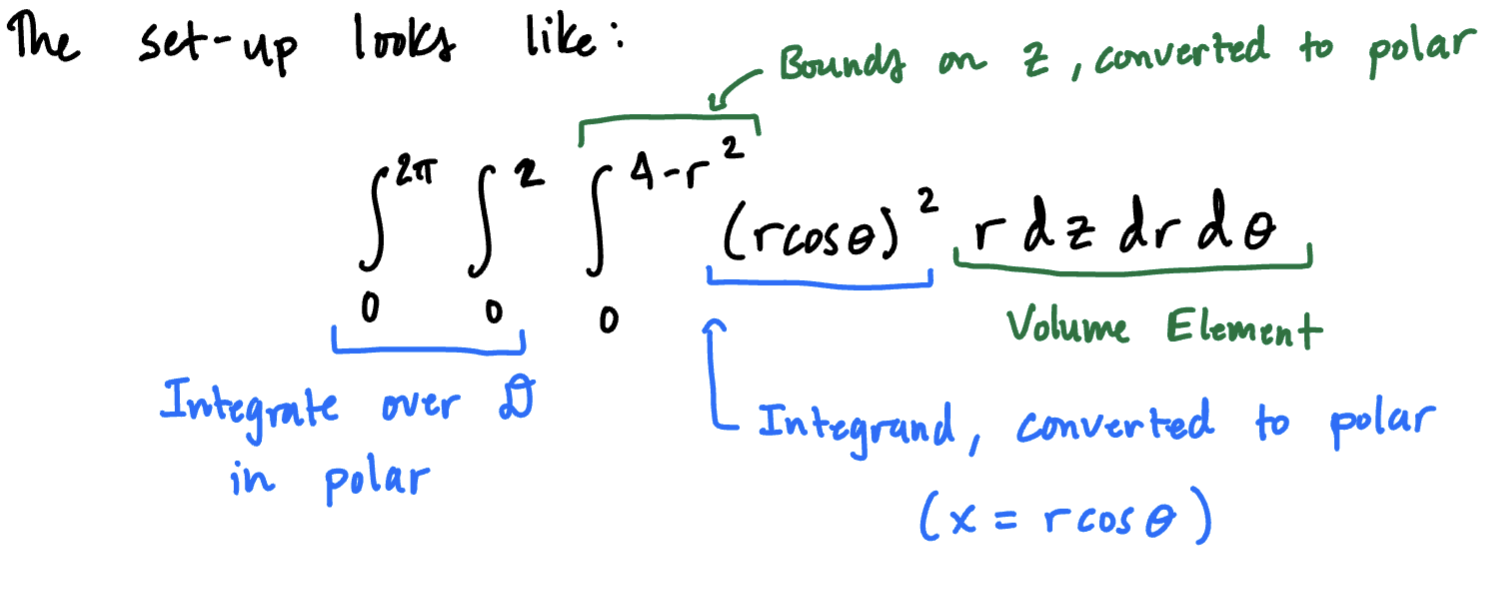
   As a Type 1 region, $0\le z\le 4-x^2-y^2$. In cylindrical coordinates, $x^2+y^2=r^2$, so we get $0\le z\le 4-r^2$

2. Express $\mathcal{D}$ in Polar Coordinates

   The disk $x^2+y^2\le 4$ has polar bounds $0\le r\le z$, $0\le \theta \le 2\pi$

3. Set-up and evalutate the integral

Sketch

$$I_1:{\int }_0^{4-r^2}{r}^3{\cos }^2\theta dz=(4-r^2)r^3{\cos }^2\theta$$ $$=(4r^3-r^5){\cos }^2\theta$$ $$I_2:{\int }_0^2(4r^3-r^5){\cos }^2\theta dr={{\cos }^2\theta \left(r^4-\frac{r^6}{6}\right)|}_0^2$$ $$=\frac{16}{3}{\cos }^2\theta$$ $$I_3:{\int }_0^{2\pi }\frac{16}{3}{\cos }^2\theta d\theta =\frac{8}{3}{\int }_0^{2\pi }1+\cos (2\theta )d\theta$$ $$=\frac{16\pi }{3}$$