16.9 - Divergence Theorem

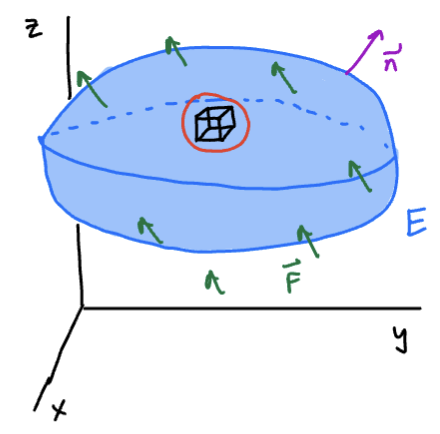
The Divergence Theorem gives us a method for computing the outward flux of $\vec{F}$ through a closed surface $S$.

Recall the flux form of Green’s Theorem (end of sec. 16.5):

$${\oint }_{\partial \mathcal{D}}\vec{F}\cdot \vec{n}ds=\int {\int }_{\mathcal{D}}div(\vec{F})dA$$

Where the $Fluxacrossboundary=SumofFluxthroughoutregion$

In the flux form of Green’s Theorem, $\vec{F}$ is a vector field on ${\mathbb{R}}^2$ and $\mathcal{D}$ is a flat surface. The divergence theorem extends this concept to vector fields on ${\mathbb{R}}^3$ and non-flat surface. Intuitively, we can arrive at this result by “increasing the dimension” of the flux form of Green’s Theorem by one: the line integral becomes a surface integral, and the double integral becomes a triple integral.

Divergence Theorem

Let $E$ be a simple solid region and let $S$ be the boundary surface of $E$. Then:

$$\int {\int }_S\vec{F}\cdot d\vec{S}=\int {\int }_E\int div(\vec{F})dV$$

Where the flux through the boundary is equal to the total flux throughout the region.

Remarks

1. A “simple” region in ${\mathbb{R}}^3$ is simultaneously Type I, II, and III. A similar condition was required for Green’s Theorem.
2. The moral of the divergence theorem is that we can compute the flux through $S$ by evaluating a triple integral. Oftentimes, the latter computation is easier.

We will have a look at a basic example, and then prove the theorem.

---

Example

Example

Find the flux of $\vec{F}=⟨z,y,x⟩$ across the unit sphere $x^2+y^2+z^2=1$

Solution

We solved the problem in Sec. 16.7 by directly evaluating the surface integral. The ( rather involved ) calculation showed that the flux is $\frac{4\pi }{3}$. Here we arrive at the same answer by way of the Divergence Theorem.

Using the surface integral of the sphere and the volume integral of the solid sphere:

$$\begin{array}{rl}\int {\int }_S\vec{F}\cdot dS& =\int {\int }_E\int div\vec{F}dV\\ & =\int {\int }_E\int 1dV\\ & =VolumeofE\\ & =\frac{4}{3}\pi r^3=\frac{4}{3}\pi \end{array}$$

---

Proof of the Divergence Theorem

Similar to Stokes’ Theorem, the Divergence Theorem can be understood visually and intuitively.

Sketch

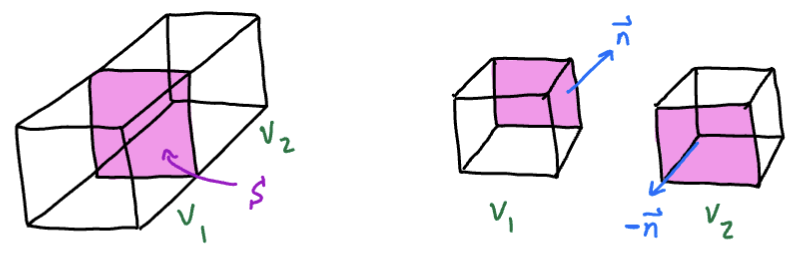
The idea is to chop up $E$ into its volume elements. The idea is to sum up the flux through each volume element.

Observe that flux cancels between adjacent volume elements:

Sketch

“Adjacent” Volume Elements share a common face.

When we find the flux through a volume element, we find the flux through each face of the box, The outward normals are exact opposites, so:

$$\begin{array}{r}Fluxthru=\int {\int }_S\vec{F}\cdot \vec{n}dS;Fluxthru=\int {\int }_S\vec{F}\cdot (-\vec{n})dS=-\int {\int }_S\vec{F}\cdot \vec{n}dS\\ Son{V}_{1}Son{V}_2\end{array}$$

When we add together these fluxes, they cancel!

Moral:

All of the flux cancels throughout the adjacent volume elements. The faces of the volume elements that do not have an adjacent counterpart form the boundary of $E$, which is the surface $S$. Therefore, all that remains is the flux through $S$:

$$\begin{array}{rl}{\int }_S\int \vec{F}\cdot dS& =\left(\begin{array}{c}sumofthefluxthrough\\ thevolumeelements\end{array}\right)\\ & \approx \sum _{j=1}^m\sum _{j=1}^n\sum _{k=1}^l(FluxthroughVolumeElementijk)\end{array}$$

---

What is the Flux through a Volume Element?

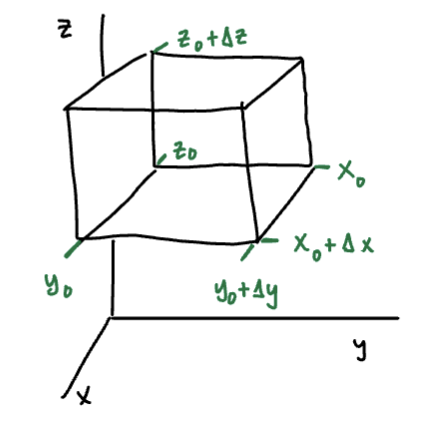
Consider a volume element with one corner at $(x_0,y_0,z_0)$ and dimensions $\Delta x,\Delta y,\Delta z$. The flux through this element is the sum of the flux across each face.

Sketch

We’ll find the flux across the front and back faces. The other faces follow a similar pattern.

Back Face

This face lies in the plane $x=x_0$ and the outward unit normal is, trivially, $\vec{n}=⟨-1,0,0⟩$. The flux is calculated directly as:

$$\begin{array}{rl}Flu{x}_1=\int {\int }_S\vec{F}\cdot \vec{n}dS& ={\int }_{\mathcal{D}}\int ⟨P,Q,R⟩\cdot ⟨-1,0,0⟩dA\\ & ={\int }_{\mathcal{D}}\int -P(x_0,y,z)dA\\ wecanapproximateoverasmallregion& \\ & =-P(x_0,y_0,z_0){\int }_{\mathcal{D}}\int dA\\ theremainingintegralistheareaoftheface\Delta y\Delta z& \\ & =-P(x_0,y_0,z_0)\cdot \Delta y\Delta z\end{array}$$

Front Face

This face lies in the plane $x=x_0+\Delta x$, and the unit normal is $\vec{n}=⟨1,0,0⟩$. Therefore:

$$\begin{array}{rl}Flu{x}_2=\int {\int }_S\vec{F}\cdot \vec{n}dS& ={\int }_{\mathcal{D}}\int ⟨P,Q,R⟩\cdot ⟨1,0,0⟩dA\\ & ={\int }_{\mathcal{D}}\int P(x_0+\Delta x,y,z)dA\\ & \approx P(x_0+\Delta x,y_0,z_0)\Delta y\Delta z\end{array}$$

Adding together $Flu{x}_1$ and $Flu{x}_2$

$$\begin{array}{rl}Flu{x}_1+Flu{x}_2& =P(x_0+\Delta x,y_0,z_0)\Delta y\Delta z-P(x_0,y_0,z_0)\Delta y\Delta z\\ & =\frac{[P(x_0+\Delta x,y_0,z_0)-P(x_0,y_0,z_0)]}{\Delta x}\Delta x\Delta y\Delta z\\ & \approx P_x(x_0,y_0,z_0)\Delta x\Delta y\Delta z\\ & =P_x\Delta V\end{array}$$

A similar analysis reveals:

$$Fluxthruleft+Fluxthruright=Q_y\Delta V$$ $$Fluxthrutop+Fluxthrubottom=R_z\Delta V$$

Adding up the Flux Through All 6 Faces Yields:

$$(Fluxthruvolumeelement)=(P_x+Q_y+R_z)\Delta V=(div\vec{F})\Delta V$$

Subbing this into the sum from the Moral, and taking the limit ${\lim }_{m,n,l\to \infty }$ gives us the divergence theorem:

$$\int {\int }_S\vec{F}\cdot d\vec{S}=\int {\int }_E\int div(\vec{F})dV\square$$