Moving on to chapter 2, we will discuss the concept of probability. Probability is a fundamental concept in statistics that quantifies the likelihood of an event occurring. Understanding probability is essential for making informed decisions based on data and statistical analyses.
2.1 Ratio
“probability of event A occurring”
We can find the axioms for probability in the following:
Using the last two, how can we find the null set ?
Well, and are complements of each other.
By complementation:
Union, Inclusive OR
Gradual Addition Rule:
Lets say that a set is a collection of disjoint events.
Then:
if all A,B disjoint, then:
When you don’t have disjoint events, we use the inclusion-exclusion principle:

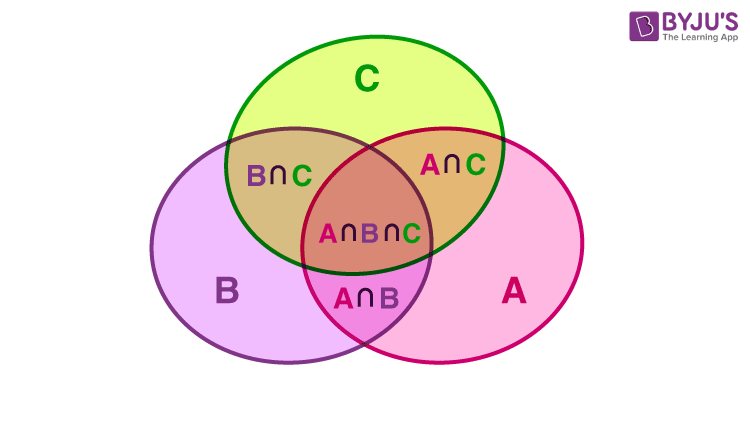
This can be extrapolated to three circles:
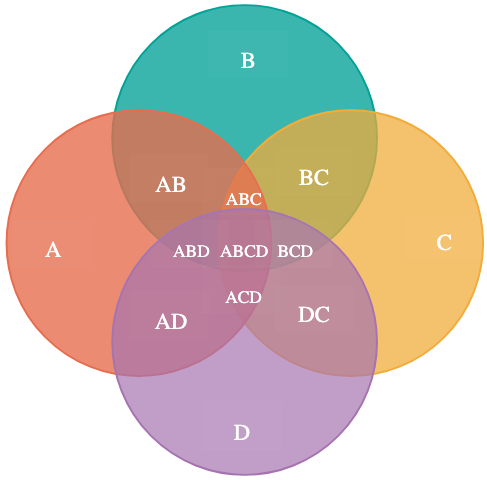
And for the sake of it, let’s do 4 circles, and we will expand out the full probability this time:
A Very Big Example
Example
A song is chosen at random from a perosn’s mp3 player. The student makes a partition of the sample space, according to genre of music. The table below gives the number of outcomes in each part of the partition. There are 27,333 songs altogether.
| 1032 Alternative | 83 Electronic | 56 Metal |
|---|---|---|
| 330 Blues | 508 Folk | 2718 Other |
| 275 Books and Spoken | 183 Gospel | 1786 Pop |
| 1468 Childrens Music | 82 Hop Hop | 403 R and B |
| 921 Classical | 564 Holiday | 8286 Rock |
| 6169 Country | 537 Jazz | 1432 Soundtrack |
| 178 Easy Listening | 106 Latin | 216 World |
| **Let A be the event that a song is either blues, jazz or rock; i.e., A = {X | x is blues, jazz, or rock song} when one song is chosen at random. Assume that all songs are equally likely to play.** |