We will be evaluating double integrals as iterated integrals. We will explain why shortly, but first we will explain how iterated integrals work.
Iterated Integrals Definitions
An integral of the following form
Means that we integrate with respect to y ( holding x fixed ) from c to d, and integrate the result with respect to x from a to b
However…
An integral with this form
Means something something a little similar, except that we integrate with respect to x, and then with respect to y.
Basic Example
Integrate first with respect to y
FTC with y=1, y=2
Simplify and integrate with respect to x
Leaving us with our final answer
What if We Reverse the order of Integration?
Instead of doing it how we just did, we will instead evaluate the inner integral , inside of the outer integral limits.
Proof of Fubini’s Theorem
Imagine a 3D graph where:
Sketch
Alternative, but incomplete python graph
Another way we can calculate the volume integral (as an alternative to Riemann sums) is by adding up vertical slabs parallel to the x-axis. If we partition the interval on the y-axis into n sub-intervals of width:
we get:
The volume of the slab is the area of the “front face” (face on the right in the figure) times the width. But the area of the front face is merely the area under the trace curve obtained by intersecting the surface with the plane in other words, a 2D integral. So:
This means the total volume is approximately:
Intuitively, the volume is exact in the limit :
By definition of the Riemann integral:
A similar argument using slabs parallel to the y-axis shows:
and because earlier we defined
the result is proved.
Remark on the Area Element
Fubini’s Theorem reveals the the rectangular area element is equal to
This aligns with the derivation at the beginning of these notes. If we partition into m sub-intervals of width , and into n sub-intervals of width , then the area of each (see the stencil) is .
Example
Example
Find the volume of hte solid that lies above the rectangle
and below the elliptic paraboloid
Solution
In 15.1, we estimated the volume with Mathematica. Here, we find it exactly using Fubini’s Theorem.
A clean way to organize our work is by evaluating the inner integral (call it ) separately, then handling the outer integral (call it ).
For
For
Remark
Order of integration doesn’t matter … we could have integrated with respect to y first.
Example
Evaluate:
Where:
Solution
We have to be wise when choosing the order of integration. Here, we should integrate with respect to x first, because the integral with respect to y requires integration by parts.
Integrate first with respect to X
From here, you can already tell its zero…
Interpretation
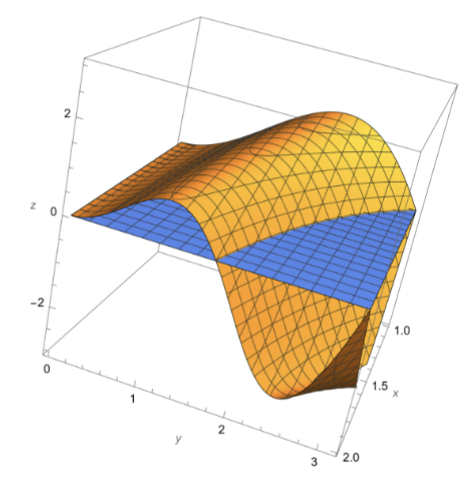
Graph
We can interpret these integrals as “signed volume.” In this example, the volume above the xy-plane is equal to the volume below the xy-plane. But volume beneath the xy-plane is considered “negative”, so the two volumes cancel.
Example of “Constant” Trickery
If , then:
Observe
is a constant with respect to , so we can write:
By the linearity of the integral
But when we evaluate the inner integral, we’ll get a constant, which will move through the outer integral. We’ll be left with:
Moral
If the integrand of an iterated integral can be factored into two functions dependent only on different variables, then we can evaluate the iterated integral as a product of two “standard” integrals: