Neuron

The Structure of a Neuron in Neural Networks

Overview

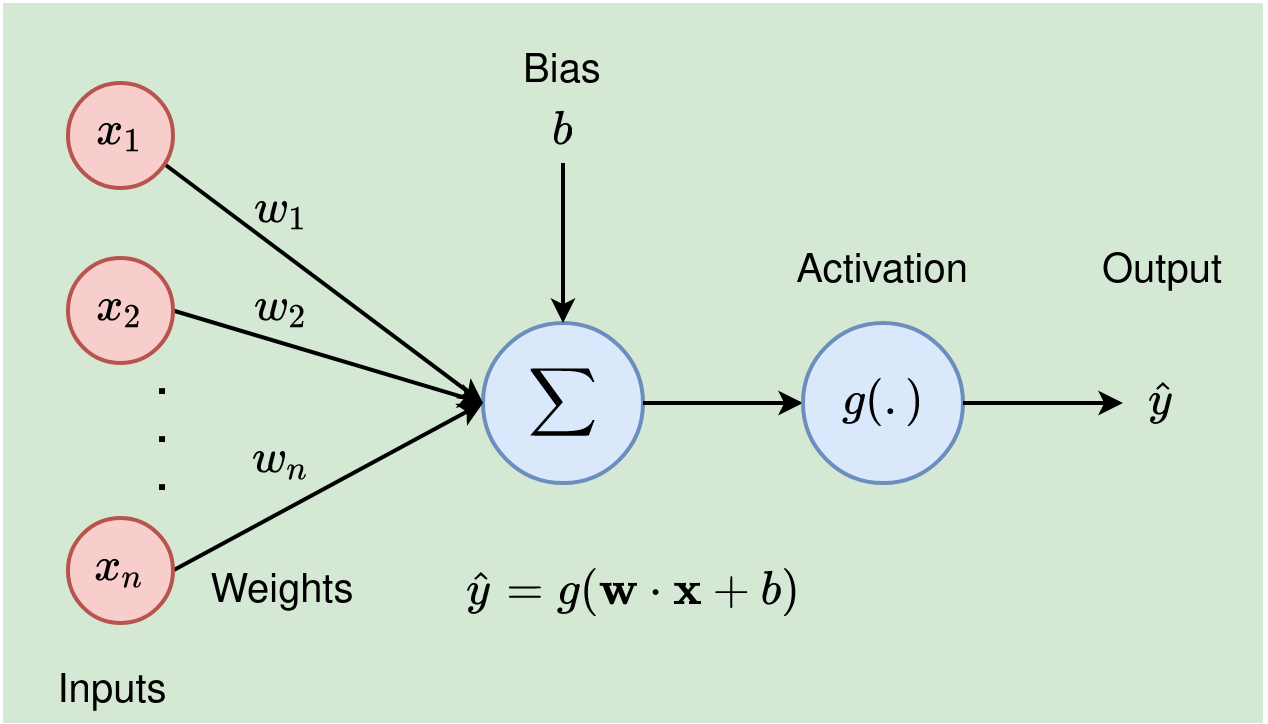
In neural networks, a neuron (also called a node or unit) is the fundamental building block that processes information. Inspired by the biological neurons in the human brain, artificial neurons take in inputs, apply transformations using weights and biases, and then pass the result through an activation function to produce an output.

Components of a Neuron

1. Inputs

   • Neurons receive multiple inputs, often denoted as x₁, x₂, ..., xₙ.
   • These inputs typically represent features from the data or outputs from other neurons in a previous layer.

2. Weights

   • Definition: Weights (w₁, w₂, ..., wₙ) are parameters that determine the importance of each input.
   • Role: Each input is multiplied by its corresponding weight before being summed. The weights are learned during the training process to minimize the error in the model’s predictions.

   Weighted Sum Example:
   If a neuron has inputs x₁, x₂, ..., xₙ and corresponding weights w₁, w₂, ..., wₙ, the weighted sum can be represented as:

   z = w₁x₁ + w₂x₂ + ... + wₙxₙ

3. Bias

   • Definition: Bias (b) is an additional parameter added to the weighted sum of inputs.
   • Role: The bias allows the model to shift the activation function left or right, which helps the model fit the data better. It acts as an intercept in linear equations.

   Final Sum Example:
   The bias is added to the weighted sum to get the final value:

   z = w₁x₁ + w₂x₂ + ... + wₙxₙ + b

4. Activation Function

   • Definition: After computing the weighted sum (with bias), the neuron applies an activation function to this sum.
   • Role: The activation function introduces non-linearity into the model, allowing the neural network to learn complex patterns. Without it, the model would be equivalent to a simple linear regression model, regardless of its depth.

   Common Activation Functions:

   • Sigmoid: Squashes the output to a range between 0 and 1.
   • ReLU: Outputs the input directly if positive, otherwise, it outputs zero.
   • Tanh: Squashes the output to a range between -1 and 1.
   • Softmax: Converts the outputs into probabilities that sum to 1 (typically used in the output layer for classification).

5. Output

   • Definition: The output of a neuron is the final result after applying the activation function.
   • Role: This output can be passed as an input to neurons in subsequent layers or be used directly as the prediction in the case of the output layer.

   Output Example:
   If f represents the activation function, the output of the neuron is:

   output = f(z) = f(w₁x₁ + w₂x₂ + ... + wₙxₙ + b)

Summary of the Neuron’s Process

1. Input Reception: The neuron receives multiple inputs.
2. Weight Application: Each input is multiplied by its corresponding weight.
3. Bias Addition: The bias term is added to the weighted sum.
4. Activation: The sum is passed through an activation function.
5. Output: The neuron produces an output that is used by subsequent neurons or layers.

Importance in Neural Networks

The structure of a neuron is central to how neural networks learn and make predictions. By adjusting weights and biases during training, the network can learn to model complex relationships in data. The activation function allows the network to capture non-linear patterns, making the model more powerful and capable of handling a wide variety of tasks.