Day 1

This class will discuss important concepts such as what can be computed, automata, and what is considered a model of computation.

This note serves as a launching pad for the rest of the course. It will introduce the concepts that will be discussed in the following classes.

---

What Can Be Computed?

And different models of computation

“what can be computed” is a question that has been asked for centuries. The answer to this question has evolved over time, where we have seen the development of different models of computation. These models of computation are used to understand the limits of computation and to understand what can be computed.

• Deterministic finite automata
  • pattern matching, ex. REGEX
• Nondeterministic finite automata
• Context-free grammars
• Pushdown automata
• Linear boundaries
• Turing machines
  • Turing machines will be discussed in more detail in a following class.

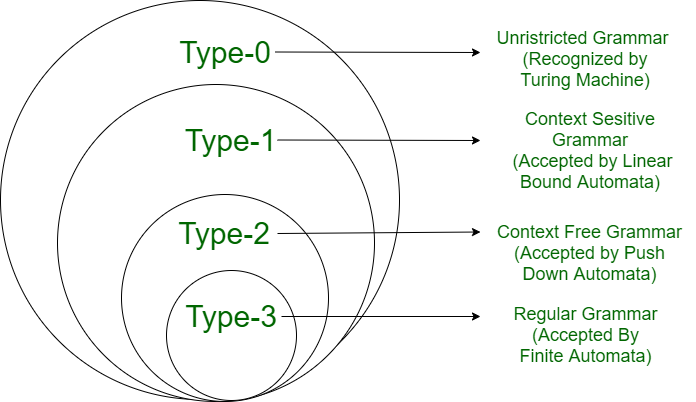
Context-Free Languages are languages that can be recognized by a pushdown automaton. These languages are used in programming languages, such as C, Java, and Python.

Context-Sensitive Languages are languages that can be recognized by a linear-bounded automaton.

---

Languages

A language is a set of strings, where a string is a sequence of symbols. For example, the set of all strings that contain only the symbols 0 and 1 is a language.

Chomsky Hierarchy

While Noam Chomsky is not computer scientist, he is known for his work in linguistics. His work has been applied to computer science, where he developed the Chomsky hierarchy. The Chomsky hierarchy is a classification of formal languages based on their generative power.

---

Complexity

There are a few terms we should familliariase ourselves with:

• P - Polynomial time
• NP - Nondeterministic polynomial time
• PSPACE - Polynomial space
• NP Hard - A problem is NP Hard if every problem in NP can be reduced to it in polynomial time.

---

Proofs

Since this should be considered more of a math class, a lot of what we will be doing will be writing proofs to show that certain problems are in a certain class.

When we are asked to prove something, we have a few options:

• proof by construction
• proof by contradiction
• proof by induction

Proof by Consituction

This is where we show that a solution exists by constructing it.

This could be something like “Show language A is regular by constructing a DFA that recognizes it.”

$$\{w|length(w)\text{ is even}\}$$

Proof by Contradiction

This is where we assume the opposite of what we want to prove and show that it leads to a contradiction.

Contradiction is to show that some language is not T-recognizable.

Suppose the language is recognizable by a Turing machine. Then we can construct a Turing machine that recognizes the complement of the language. This would lead to a contradiction.

Proof by Induction

This is where we show that a statement is true for all natural numbers.

Suppose we want to show that a language is regular. We can show that the language is regular for the base case, and then show that if the language is regular for some n, then it is regular for n+1.

---

Boolean Logic and LaTeX Definitions

Let’s familiarize ourselves wtih some of the boolean connectives and their latex counterparts.

• AND: $\wedge$ aka conjunction
• OR: $\vee$ aka disjunction
• NOT: $\neg$
• IMPLIES: $⟹$
• IFF: $⟺$
• XOR: $\oplus$

More so, lets practice some truth tables to make sure we are still familiar with them.

P	Q	P $\wedge$ Q	P $\vee$ Q	P $⟹$ Q	P $⟺$ Q	P $\oplus$ Q
T	T	T	T	T	T	F
T	F	F	T	F	F	T
F	T	F	T	T	T	T
F	F	F	F	T	T	F

De Morgan’s Laws

I am sure we are all familiar with this law by now, but heres the logical definition:

$$\neg (P\wedge Q)⟺\neg P\vee \neg Q$$ $$\neg (P\vee Q)⟺\neg P\wedge \neg Q$$

Sets

Sets are a collection of elements. We can define sets using set builder notation.

Sets can be defined like so:

$$\{a,b,c\}$$ $$\{1,2,3,\dots ,n\}$$

Sets cannot be defined in a disordered manner. For example, the following is not a set:

$$\{Tuesday,42,Jim,\dots \}$$

We can also define a set with some logic:

$$A=\{w||w|=1med2\}$$

$01\notin A$

$111\in A$

In addition we also have a few kinda of sets:

• Finite Set: A set with a finite number of elements.
• Infinite Set: A set with an infinite number of elements.

An important Reminder...

At least for this class, infinity comes in multiple sizes. For example, the set of natural numbers is infinite, but the set of real numbers is a larger infinity. For now we only have to be aware of two kinda of infinities:

• Countable Infinity: Can be put into a one-to-one correspondence with the natural numbers. untable Infinity**: Cannot be put into a one-to-one correspondence with the natural numbers.

Order of Sets

Sets are by default unordered.

$$\{a,b,c\}=\{b,c,a\}$$

If you want an ordered set, you can use a tuple.

$$(a,b,c)\ne (b,c,a)$$

More Symbol Definitions

We have a few symbols to represent things that occur enough that we should be familiar with them.

• Natural Numbers: $\mathbb{N}$: $\{1,2,3,\dots \}$
• Integers: $\mathbb{Z}$: $\{\dots ,-2,-1,0,1,2,\dots \}$
• Rational Numbers: $\mathbb{Q}$: $\{\frac{a}{b}|a,b\in \mathbb{Z}\}$
• Real Numbers: $\mathbb{R}$: $\{\text{all numbers}\}$

---

Subsets

• A is a subset of B(possibly A=B): $A\subseteq B$
  • iff every element of A is also an element of B
• A is a subset of B and A is not equal to B: $A⊊B$
  • iff every element of A is also an element of B and there is at least one element in B that is not in A
• A is a proper subset of B: $A\subset B$
  • iff every element of A is also an element of B and there is at least one element in B that is not in A

Even More Symbols

• Empty Set: $\varnothing$

---

Deterministic Finite Automata

A deterministic finite automata is defined as a 5-tuple $(Q,\Sigma ,\delta ,q_0,F)$ where:

• $Q$ is a finite set of states
• $\Sigma$ is a finite set of input symbols
• $\delta$ is the transition function
• $q_0$ is the start state
• $F$ is the set of accept states

Deterministic finite automata are used to recognize regular languages, but they are not powerful enough to recognize context-free languages.

An example of a DFA is a vending machine. The vending machine has a finite number of states, and it accepts a finite number of inputs. The vending machine has a transition function that determines what state it will go to next based on the input. The vending machine has a start state and an accept state.

Cartesian Product

The cartesian product of two sets $A$ and $B$ is the set of all ordered pairs $(a,b)$ where $a\in A$ and $b\in B$.

An example of a cartesian product is the set of all possible outcomes of a dice roll. The set of all possible outcomes of a dice roll is the cartesian product of the set of all possible outcomes of the first die and the set of all possible outcomes of the second die.

Let’s say that:

$$\begin{array}{rl}A& =\{1,2,3\}\\ B& =\{Red,Green,Blue\}\\ C& =\{Car,Motorcycle,Bicycle\}\end{array}$$

The cartesian product of $A$, $B$, and $C$ is:

$$A\times B\times C=\{(1,Red,Car),(1,Red,Motorcycle),(1,Red,Bicycle),\dots \}$$