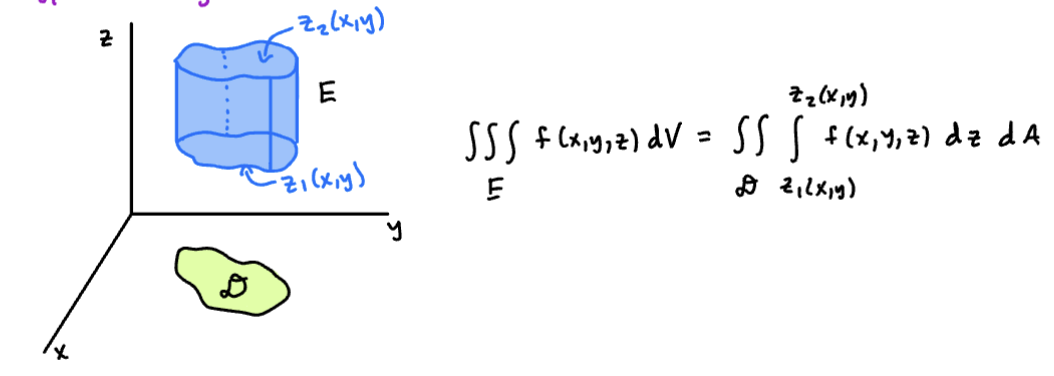15.6 - Triple Integrals

Suppose the rectangular box $E=[a,b]\times [c,d]\times [r,s]$ has a density function $p(x,y,z)$, meaning that at the points $(x,y,z)$ in $E$, the density is $p(x,y,z)$, where density means units of mass per unit of volume. $(p=\frac{m}{v})$

---

Triple Integrals

Now, we define the triple integral:

$$\int \int {\int }_{E}p(x,y,z)dV$$

In complete analogy with Riemann Sums in single and double integrals, we sub-divide $E$ into $m\times n\times \lambda$ sub-boxes:

Sketch

We know the Riemann Sum will look like:

$$\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^{\lambda }p(x^{\ast },y^{\ast },z^{\ast })\nabla V$$

Interpretation

In $(sub-box{)}_{ijk}$, $p(x^{\ast },y^{\ast },z^{\ast })$ is the density at point $(x^{\ast },y^{\ast },z^{\ast })$, and $\nabla V$ is the volume element, the volume of the sub-box. The summand can therefore be interpreted as:

$p(x^{\ast },y^{\ast },z^{\ast })\nabla V=(Density)(Volume)=Mass$

In the Riemann Sum, we are adding up the mass of the volume elements, approaching the total mass as $m_1{n}_1\lambda \to \infty$.

---

Three-Dimensional Volume Element

Sketch

---

Triple Integrals over “Rectangular” Regions

The triple integral of $f(x,y,z)$ over $E=[a,b]\times [c,d]\times [r,s]$ is:

$$\int \int {\int }_{E}f(x,y,z)dV=\underset{m,n,\lambda \to \infty }{\lim }\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^{\lambda }f(x^{\ast },y^{\ast },z^{\ast })\nabla V$$ $$={\int }_a^b{\int }_c^d{\int }_r^{s}f(x,y,z)dzdydx$$

Remarks

1. The interpretation is mass (discussed above), or “hyper-volume” between the surface $f(x,y,z)$ (in 4D) and integration region E
2. Fubini’s Theorem still holds, but now there are six orders of integration: $dxdydz,dxdz,dy,dydxdz,dydz,dx,dzdz,dy,dzdydx$
3. We calculate the integrated integrals like before ,but with one more iteration.

---

Triple Integrals over General Regions

Most regions we encounter will be non-rectangular and simple.

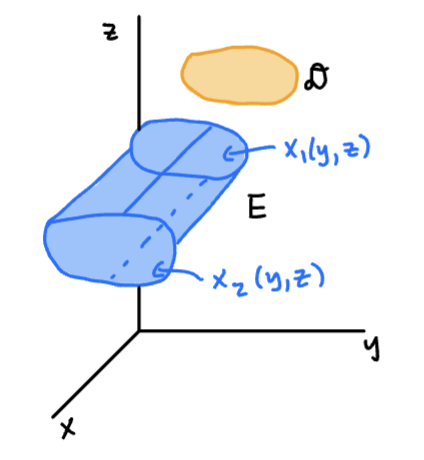
Type 1 Region

A Type 1 region is contained between two continuous surfaces $z_1(x,y)$ and $z_2(x,y)$. $\mathcal{D}$ is the projection of E onto the xy-plane. We integrate out z by running between the surfaces $z_1$ and $z_2$, then integrate over the region $\mathcal{D}$, using techniques we have from double integration.

Example

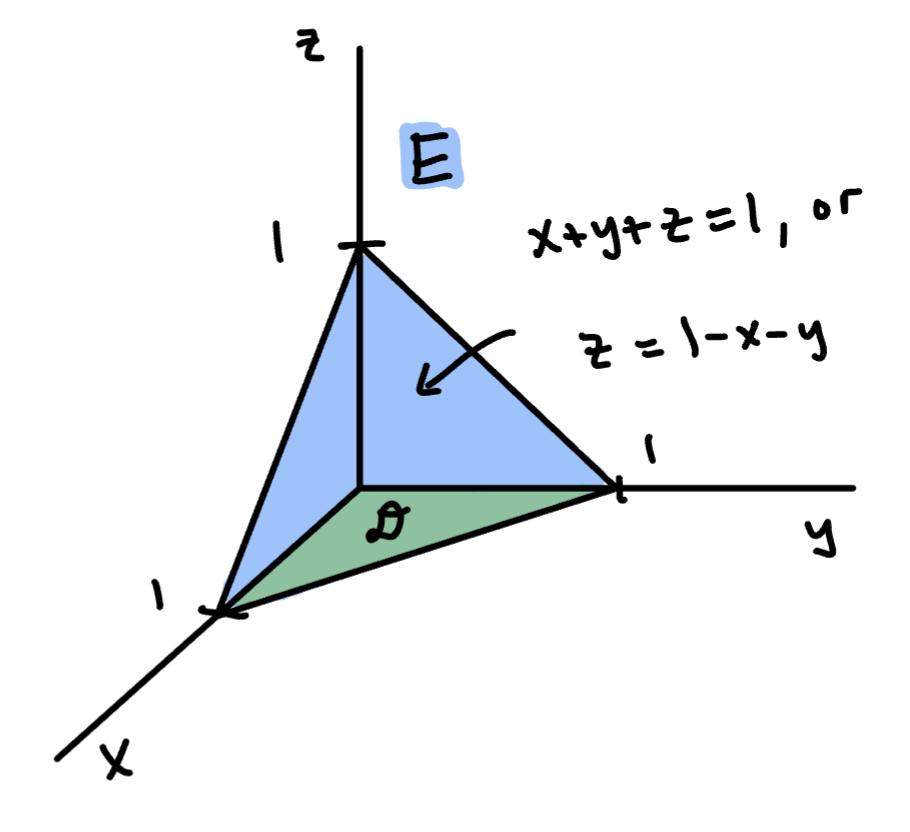
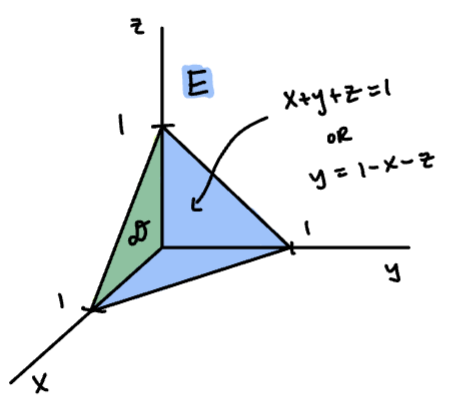
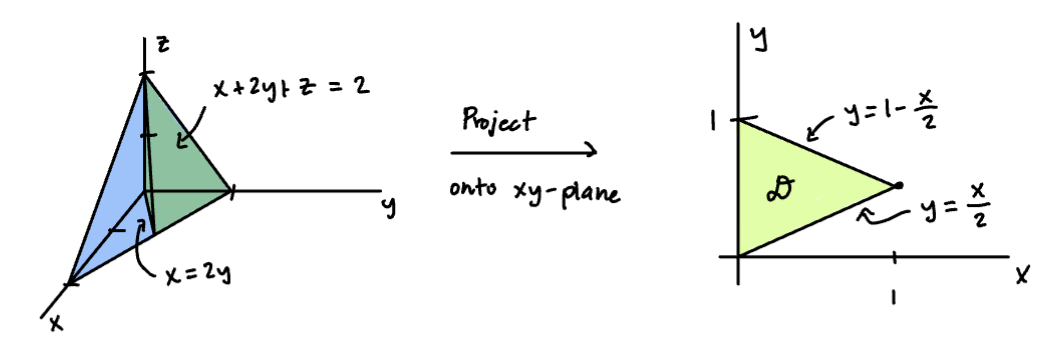
Evaluate $\int \int {\int }_{E}zdV$, where E is the solid tetrahadron bounded by the planes $x=0$, $y=0$, $z=0$, and $x+y+z=1$.

Solution

Always sketch the solid E.

Sketch

E is bounded between the planes $z=0$ and $z=1-x-y$, so it’s a Type 1 region. By the above formula,

$$\int \int {\int }_{E}zdV=\int {\int }_{\mathcal{D}}{\int }_0^{1-x-y}zdzdA$$

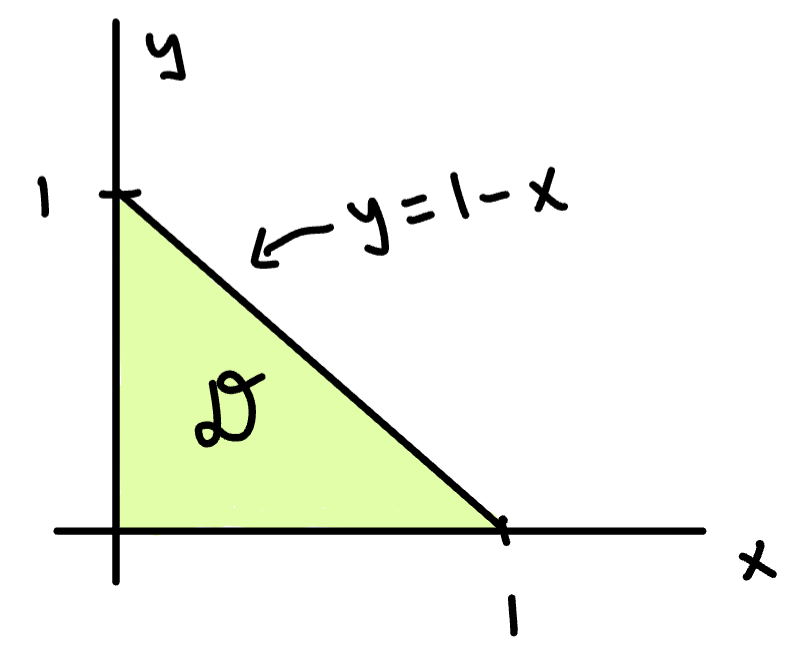
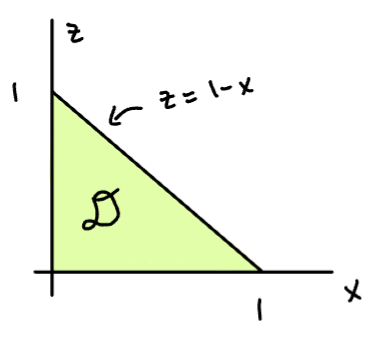
Sketch $\mathcal{D}$, the projection of E onto the xy-plane.

Sketch

$\mathcal{D}$ is a Type 1 region:

$$0\le x\le 1,0\le y\le 1-x$$

We can now write the integral as:

$$\int \int {\int }_{E}zdV=\int {\int }_{\mathcal{D}}{\int }_0^{1-x-y}zdzdA={\int }_0^1{\int }_0^{1-x}{\int }_0^{1-x-y}zdzdydx$$

To show how the triple integration works, we carry out $I_1$ ( of 3 ):

$$I_1:{\int }_0^{1-x-y}zdz={\frac{z^2}{2}|}_0^{1-x-y}=\frac{(1-x-y{)}^2}{2}$$

The problem is now the double integral

$${\int }_0^1{\int }_0^{1-x}\frac{(1-x-y{)}^2}{2}dydx=\frac{1}{24}$$

---

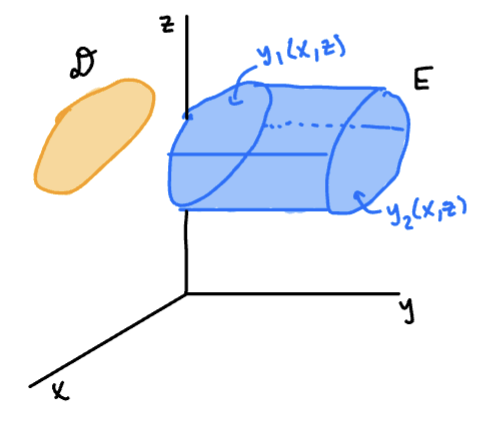
Type 2 and Type 3 Regions

Type 2

Type 2 regions are contained between a “front” and “back” surface.

$$\int \int {\int }_{E}f(x,y,z)dV=\int {\int }_{\mathcal{D}}{\int }_{x_1(y,z)}^{x_2(y,z)}f(x,y,z)dxdA$$

Type 3

Type 3 regions are contained between a “left” and “right” surface.

$$\int \int {\int }_{E}f(x,y,z)dV=\int {\int }_{\mathcal{D}}{\int }_{y_1(x,z)}^{y_2(x,z)}f(x,y,z)dydA$$

---

Example

Write the integral from the previous example in another order, integrating first with respect to y

Sketch

As a Type 3 Region:

$$0\le y\le 1-x-z$$

To get integration limits on x and y, we need to sketch $\mathcal{D}$.

Sketch

As a Type 1 region, $\mathcal{D}$ has bounds:

$$0\le z\le 1-x,0\le x\le 1$$

We can write the triple integral as:

Solution

$${\int }_0^1{\int }_0^{1-x}{\int }_0^{1-x-z}zdydzdx$$

Remark

We could also express E as a Type 2 region, or $\mathcal{D}$ as a Type 2 region; 6 possibilities in total.

---

Finding Volume with Triple Integrals

The expression:

$$\int \int {\int }_{E}1dV=\sum \sum \sum \Delta V$$

says “add up all of the volume elements in E.” Therefore:

$$\int \int {\int }_{E}1\cdot dV=V(E)=VolumeofE$$

Let’s apply this with an example.

---

Example

Find the volume of the tetrahedron bounded by the planes:

$x+2y+z=2,x=2y,x=0,andz=0$

[!Success]- Solution

We have to sketch the solid $x+2y+z=2$ in the first octant and intersect it with the plane $x=2y$

Sketch

Remark

We obtain the bounds on $\mathcal{D}$ from the sketch of the solid. The plane $x+2y+z=2$ intersects the xy-plane $(z=0)$ in the line $x+2y=2$, or $y=1-\left(\frac{x}{2}\right)$. The lower boundary comes from re-writing $x=2y$ as $y=\frac{x}{2}$

The volume is therefore:

$$V=\int \int {\int }_{E}dV={\int }_0^1{\int }_{\frac{x}{2}}^{1-\frac{x}{2}}{\int }_0^{2-x-2y}=\frac{1}{3}$$

2-x-2y comes from $x+2y+z=2;solveforZ$