14.2 - Multivariable Limits

We are all familiar with multivariable limits from calculus 2, so let’s just start with a quick refresher.

---

Refresher - Continuity

Continuity is the concept of a line having no breaks - otherwise known as a continuous flow with no disconnections.

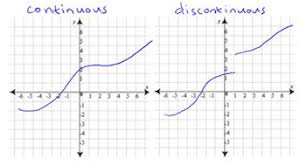
A line is continuous when it is one, smooth stroke.

A line is discontinuous when there is a visible break or “jump” in the line’s path.

---

Bringing it to 3D

In Calculus 3, continuity in the 3D space means that we can traverse a surface without interruption

• No vertical “cliffs” or “walls” or “trenches”
• No points with “infinite height/depth”

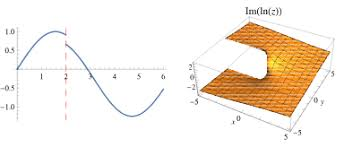
Discontinuity in 3d

---

Calculus 1 - f(x) is Continuous at A…

This usually means something like a limit of a function $f(x)$ is in of itself that limit $f(a)$,

Where:

$\lim \_x\to af(x)=f(a)$

In Calculus 3 this is expanded apon for 14.1 - Multivariable functions, where we now have to deal with functions like $f(x,y)$

How do we deal with this?

Problem

How de we show that $f(x,y)$ is continuous at $(a,b)$?

It is actually quite simple, where we just add another letter to represent its inherent multivariability.

Answer

$\lim \_(x,y)\to (a,b)f(x,y)=f(a,b)$

This introduces some interesting ideas, as there are now multiple different ways for us to reach the same answer.

As it turns out, for ${\lim }_{(x,y)\to (a,b)}f(x,y)$ , there are infinitely many ways for $(x,y)$ to approach $(a,b)$

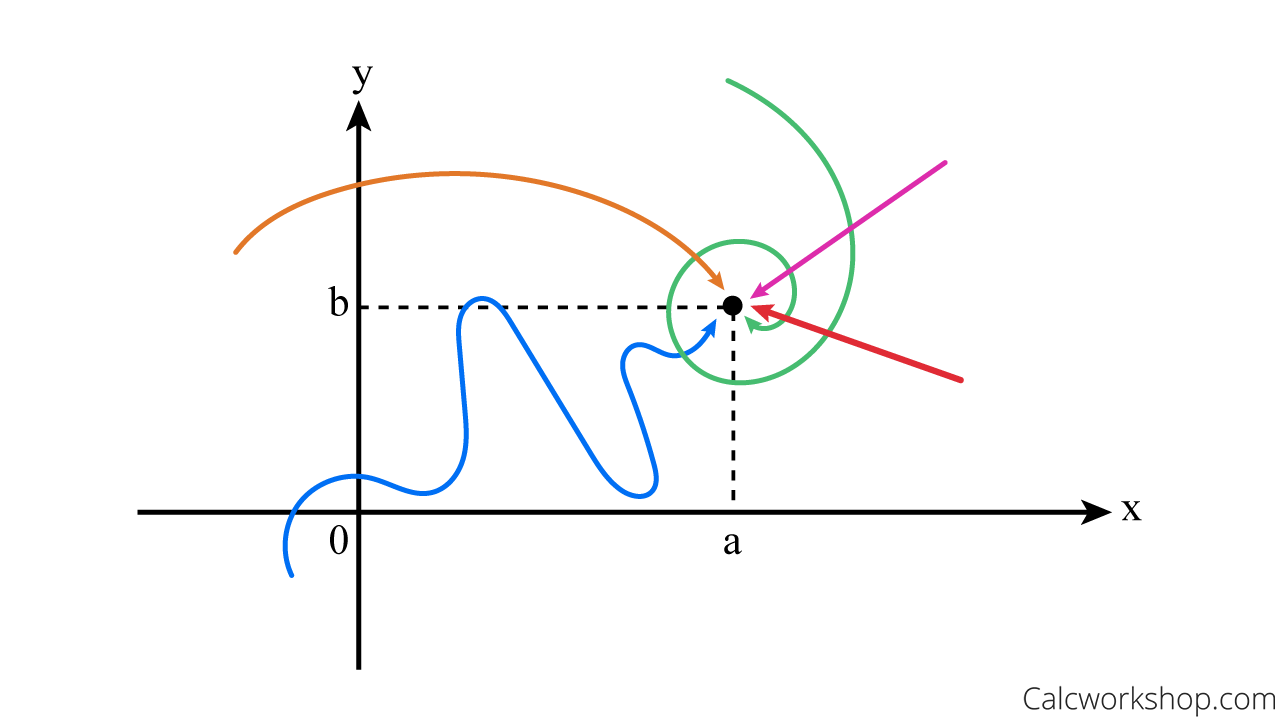
This makes proving a limit exists all the more difficult, as you now must address the following cases.

Hard

In order for a limit $L$ to exist, $f(x,y)$ must approach L as $(x,y)$ approaches $(a,b)$ along every path towards $(a,b)$

However, this also makes proving a limit is DNE a lot simpler.

To show a limit is DNE

• find 2 paths whose limits disagree