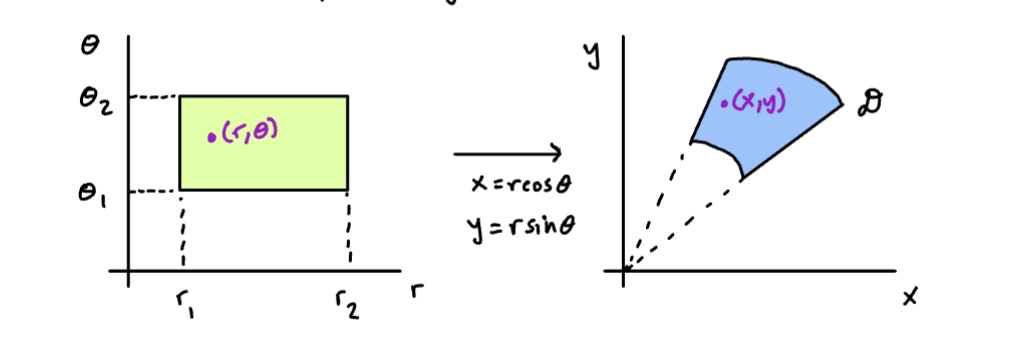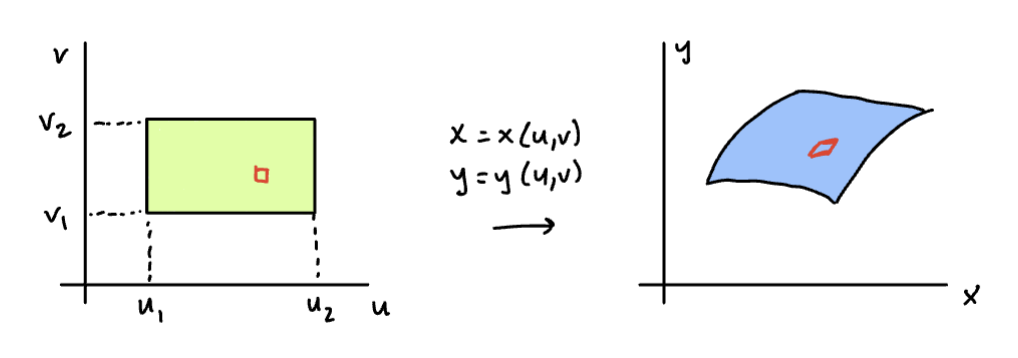15.9 - Jacobian

Polar, cylindrical, and spherical coordinates area form of substitution in multiple integrals. Let’s recall how Polar works:

Sketch

If $\mathcal{D}$ is a polar region,

$${\int }_{\mathcal{D}}\int f(x,y)dA={\int }_{{\theta }_1}^{{\theta }_2}{\int }_{r_1}^{r_2}f(r\cos \theta ,r\sin \theta )dA$$

We know the area element is $dA=rdrd\theta$. The integration limits, $r_1\le r\le r_2$ and ${\theta }_1\le \theta \le {\theta }_2$, correspond to a rectangle in the $r\theta$-plane.

In this document, we will learn how to find the area element/volume element, also known as the Jacobian Determinant, in the general case where the change of variable is given by $x=x(u,v),y=y(u,v)$.

---

Deriving the Area Element

Suppose the rectangular region $[u_1,u_2]$, $[v_1,v_2]$ in the uv-plane corresponds to some integration region in the xy-plane under the substitution $x=x(u,v)$, $y=y(u,v)$.

Sketch

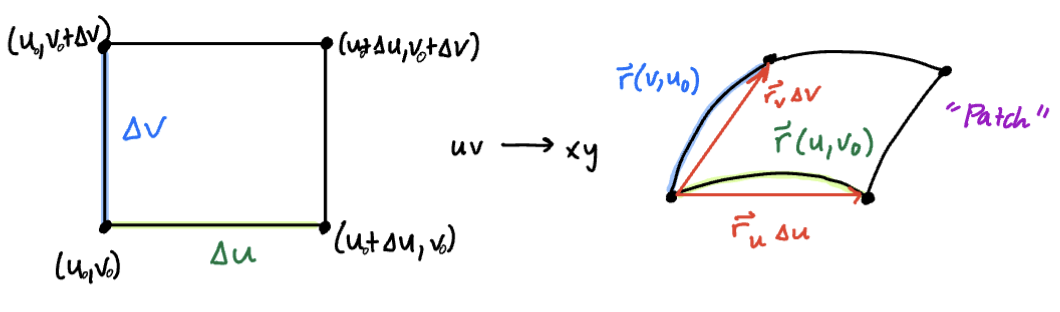
The rectangle with dimensions $\Delta u\Delta v$ (the red square in the figure) in the uv-plane corresponds to a patch (the red parallelogram) in the xy-plane.

Sketch

Suppose the red rectangle has bottom-left corner $(x_0,y_0)$. Suppose the point $(x,y)$ is obtained by $\vec{r}(x(u,v),y(u,v))$. Along the bottom line of the rectangle, $u$ varies and $v$ is held constant; this corresponds to the vector curve $\vec{r}(u,v_0)$, where $u$ varies from $u_0$ to $u_{0}t\Delta u$.

Claim

We can approximate the segment of $\vec{r}(u,v_0)$ shown in the figure by the vector ${\vec{r}}_u(u_0,v_0)\Delta u$.

Justification

By definition of the derivative:

$$\frac{d\vec{r}}{du}={\vec{r}}_u\to \frac{\Delta \vec{r}}{\Delta u}\approx {\vec{r}}_u\to \Delta \vec{r}\approx {\vec{r}}_u\Delta u$$

Similarly, the segment of the vector curve $\vec{r}(v,u_0)$ is approximated by the vector ${\vec{r}}_v\Delta v$, because along this curve we let $v$ vary and hold $u$ constant.

The area element is the area of the patch:

$$AreaofPatch\approx Areaofparallellelogram$$ $$=|{\vec{r}}_u\Delta u\times {\vec{r}}_v\Delta v|$$ $$=|{\vec{r}}_u\times {\vec{r}}_v|\Delta u\Delta v=dA$$

Adding up the area elements and sending the number of elements to infinity yields the result:

Change of Variable in Double Integrals

Suppose the region $S$ in the uv-plane is mapped to the region $R$ in the xy-plane by $x=x(u,v)$, $y=y(u,v)$. Then:

$${\int }_R\int f(x,y)dA={\int }_S\int f(x,y)||{\vec{r}}_u\times {\vec{r}}_v||dudV$$

Where $||$ means the absolute value of $|{\vec{r}}_u\times {\vec{r}}_v|$.

Remarks

1. We need to assume continuity of $f$ and the partial derivatives ${\vec{r}}_u=⟨x_u,y_u⟩$, ${\vec{r}}_v=⟨x_v,y_v⟩$
2. The quantity $|{\vec{r}}_u\times {\vec{r}}_v|$ is called the Jacobian Determinant, which we can call $J$. In 2D, we have:

$$J=|{\vec{r}}_u\times {\vec{r}}_v|=\left|\begin{array}{ccc}i& j& k\\ x_u& y_u& 0\\ x_v& y_v& 0\end{array}\right|=\left|\begin{array}{cc}{x}_u& y_u\\ x_v& y_v\end{array}\right|$$

The Jacobian “stretches” the rectangle $\Delta u\Delta v$ to create the area element.

3. If the Jacobian is negative, we take its absolute value in the integral ( the area element is positive)

---

Examples

Example

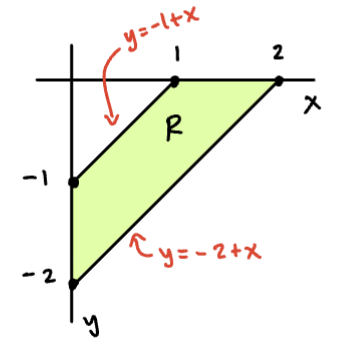
Evaluate the integral $\int {\int }_R{e}^{\frac{(x+y)}{(x-y)}}dA$, where $R$ is the trapezoidal region with vertices $(1,0),(2,0),(0,-2),(0,-1)$

Solution

A suitable change of variable appears to be $u=x+y$, $v=x-y$

Sketch

$$\left\{\begin{array}{c}x+y=u\\ x-y=v\end{array}\right\}\begin{array}{cccc}\to & 2x=u+v& \to & x=\frac{1}{2}(u+v)\\ \to & 2y=u-v& \to & y=\frac{1}{2}(u-v)\end{array}$$ $$J:\left|\begin{array}{cc}{x}_u& y_u\\ x_v& y_v\end{array}\right|=\left|\begin{array}{cc}\frac{1}{2}& \frac{1}{2}\\ \frac{1}{2}& -\frac{1}{2}\end{array}\right|=-\frac{1}{2}$$

To sketch the integration region in the uv-plane: Observe that in the xy-plane, $x-y=1$ and $x-y=2$. Therefore, we can range $v=x-y$ from $1$ to $2$.

Bounds on u: We need to understand how $R$ maps to the uv-plane under the change of variable. We have already seen that the boundary lines $y=-1+x$ and $y=-2+x$ are constants. What about the other boundary line?

$$x=0,-2\le y\le -1$$

If $x=0$, then $u=y$ and $v=-y$, so $v=-u$, where $-2\le u\le -1$ because $u=y$

$$y=0,1\le x\le 2$$

If $y=0$, $u=x$ and $v=x$, so $v=u$, where $1\le u\le 2$ because $u=x$