16.2b - Line Integrals of Vector Fields

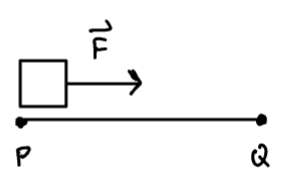
In physics, the work done by a constant force acting on an object taht moves along a line is defined by $W=Force\times Distance$.

Sketch

Where work done by $\vec{F}$ moving an object from $P$ to $Q$ is:

$$Work=|\vec{F}|\cdot |\overrightarrow{PQ}|$$

This vector $\overrightarrow{PQ}$ is called the displacement vector.

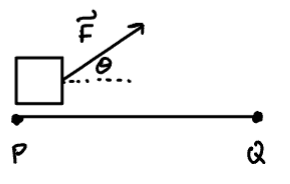
In the case where $\vec{F}$ is not parallel to $\overrightarrow{PW}$, we define:

Sketch

$$Work=|\vec{F}|\cos \theta \cdot |\overrightarrow{PQ}|$$

[^1]

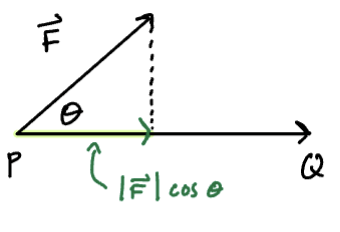
Where $\theta$ is the angle between $\vec{F}$ and $\overrightarrow{PQ}$. The interpretation of this definition is that we are multiplying the displacement vector $|\overrightarrow{PQ}|$ by the scalar projection of $\vec{F}$ onto $|\overrightarrow{PQ}|$.

Sketch

From [^1], we can write:

$$\begin{array}{rl}W& =|\vec{F}|\cdot |\overrightarrow{PQ}|\cos \theta \\ & =\vec{F}\cdot \overrightarrow{PQ}\\ & \equiv \vec{F}\cdot \vec{D}\end{array}$$

Work done by $\vec{F}$ in moving an object from $P$ to $Q$, where we define $\vec{D}=\overrightarrow{PQ}$ as the displacement vector.

---

Line Integrals of Vector Fields

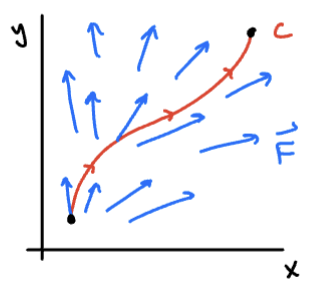
Now suppose $\vec{F}(x,y)=P(x,y)\vec{i}+Q(x,y)\vec{j}$ is a force vector field on ${\mathbb{R}}^2$. We seek to compute the work done by this force in moving a particle along a curve $C$.

Sketch

Where:

• $C$ is the curve $\vec{r}(t)=⟨x(t),y(t)⟩,t\in [a,b]$
• $\vec{F}$ is a vector field

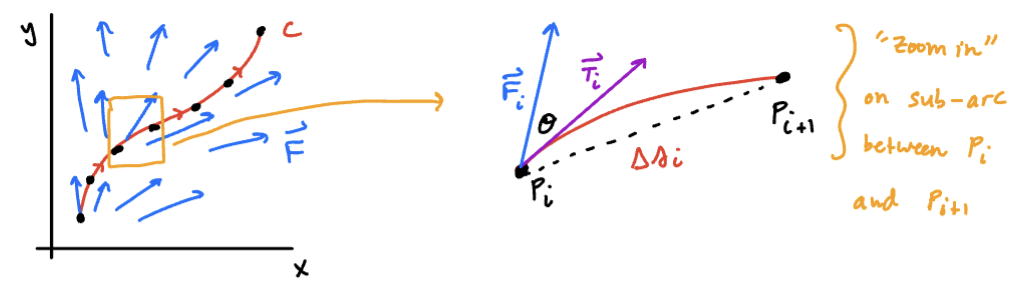
To calculate the work, we partition $C$ into n sub-areas, estimate the work done over each sub-arc, and sum them all up.

Sketch

In the right-hand image, ${\vec{F}}_i=\vec{F}(x_i,y_i)$, where $x_i=x(t_i)$ and $y_i=y(t_i)$, and ${\vec{T}}_i$ is the unit tangent vector to $\vec{r}(t)$ at $t_i$. Let $\Delta {\partial }_i$ denote the arc length of the sub-arc. As the particle moves along the curve, it moves approximately in the direction of ${\vec{T}}_i$, for a distance of $\Delta {\partial }_i$ units. We can therefore estimate the displacement vector by ${\vec{D}}_i={\vec{T}}_i\Delta {\partial }_i$.

Using the formula $W={\vec{F}}_i\cdot {\vec{D}}_i$, we find that the work done by ${\vec{F}}_i$ in moving the particle along ${\vec{D}}_i$ is:

$$W={\vec{F}}_i\cdot {\vec{T}}_i\Delta {\partial }_i\to TotalWork=\sum _{i=0}^n{\vec{F}}_i\cdot {\vec{T}}_i\Delta {\partial }_i$$ $$\to Work={\int }_c\vec{F}(x,y)\cdot \vec{T}(x,y)d\partial ={\int }_c\vec{F}\cdot \vec{T}d\partial$$

This is called a line integral of a vector field. Using:

$$\vec{T}=\frac{{\vec{r}}^{\prime }(t)}{|{\vec{r}}^{\prime }(t)|}andd\partial =|{\vec{r}}^{\prime }(t)|dt$$

we get:

$${\int }_c\vec{F}\cdot \vec{T}d\partial ={\int }_c\vec{F}\cdot \frac{{\vec{r}}^{\prime }(t)}{|{\vec{r}}^{\prime }(t)|}\cdot |{\vec{r}}^{\prime }(t)|dt={\int }_c\vec{F}\cdot {\vec{r}}^{\prime }(t)dt$$

Using the differential $d\vec{r}={\vec{r}}^{\prime }(t)dt$, we can write:

$${\int }_c\vec{F}\cdot {\vec{r}}^{\prime }(t)dt={\int }_c\vec{F}\cdot d\vec{r}$$

We summarize below:

Line Integral of a Vector Field

The line integral of $\vec{F}$ along $C$ is:

$${\int }_c\vec{F}\cdot d\vec{r}={\int }_a^b\vec{F}(\vec{r}(t))\cdot {\vec{r}}^{\prime }(t)dt={\int }_c\vec{F}\cdot \vec{T}d\partial$$

where $\vec{r}(t)$, $t\in [a,b]$ parameterizes $C$.

---

Remarks

1. The notation $\vec{F}(\vec{r}(t))$ is a shorthand. For example, if $\vec{F}=\vec{F}(x,y)$ and $\vec{r}(t)=⟨x(t),y(t)⟩$, then $\vec{F}(\vec{r}(t))=\vec{F}(x(t),y(t))$.
2. The physical analogy of the vector line integral is the work done by the vector field in moving a particle along a curve.
3. Observe: if $\vec{F}=P\vec{i}+Q\vec{j}+R\vec{k}$ and $d\vec{r}=⟨dx,dy,dz⟩$:

$$\begin{array}{rl}\vec{F}\cdot d\vec{r}& =⟨P,Q,R⟩\cdot ⟨dx,dy,dz⟩\\ & =Pdx+Qdy+Rdz\end{array}$$

Thus, vector line integrals can be broken down into line integrals with respect to $x,y,z$, etc.