Sorting Algorithms

Sorting algorithms serve as one of the most fundamental components within modern software infrastructure. Many data structures and other algorithms rely on the data being sorted, and being able to do that either quickly, efficiently, or safely cannot be undermined.

---

Quick Sort

Quick Sort is a divide-and-conquer algorithm that selects a “pivot” element and partitions the array around the pivot, sorting the elements.

Steps

1. Choose a pivot element.
2. Partition the array such that elements less than the pivot are on the left and elements greater are on the right.
3. Recursively apply the same logic to the subarrays.

Animation

C++ Implementation

#include <vector>
#include <algorithm>
using namespace std;
 
int partition(vector<int>& arr, int low, int high) {
    int pivot = arr[high];
    int i = low - 1;
 
    for (int j = low; j < high; j++) {
        if (arr[j] <= pivot) {
            i++;
            swap(arr[i], arr[j]);
        }
    }
    swap(arr[i + 1], arr[high]);
    return i + 1;
}
 
void quickSort(vector<int>& arr, int low, int high) {
    if (low < high) {
        int pi = partition(arr, low, high);
 
        quickSort(arr, low, pi - 1);
        quickSort(arr, pi + 1, high);
    }
}

Complexity

Time: $O(n\log n)$ (average), $O(n^2)$ (worst-case)
Space: $O(\log n)$ (stack space)

---

Selection Sort

Selection Sort repeatedly selects the smallest element from the unsorted portion and moves it to the sorted portion.

Steps

1. Find the smallest element in the array.
2. Swap it with the first unsorted element.
3. Repeat for the remaining unsorted portion.

Animation

C++ Implementation

using namespace std;
 
void selectionSort(vector<int>& arr) {
    int n = arr.size();
    for (int i = 0; i < n - 1; i++) {
        int minIdx = i;
        for (int j = i + 1; j < n; j++) {
            if (arr[j] < arr[minIdx]) {
                minIdx = j;
            }
        }
        swap(arr[i], arr[minIdx]);
    }
}

Complexity

Time: $O(n^2)$
Space: $O(1)$

---

Merge Sort

Merge Sort is a divide-and-conquer algorithm that splits the array into halves, sorts each half, and then merges them back together.

Steps

1. Divide the array into two halves.
2. Recursively sort each half.
3. Merge the two sorted halves.

Animation

C++ Implementation

using namespace std;
 
void merge(vector<int>& arr, int left, int mid, int right) {
    vector<int> temp;
    int i = left, j = mid + 1;
 
    while (i <= mid && j <= right) {
        if (arr[i] <= arr[j])
            temp.push_back(arr[i++]);
        else
            temp.push_back(arr[j++]);
    }
 
    while (i <= mid) temp.push_back(arr[i++]);
    while (j <= right) temp.push_back(arr[j++]);
 
    for (int k = left; k <= right; k++)
        arr[k] = temp[k - left];
}
 
void mergeSort(vector<int>& arr, int left, int right) {
    if (left < right) {
        int mid = left + (right - left) / 2;
 
        mergeSort(arr, left, mid);
        mergeSort(arr, mid + 1, right);
        merge(arr, left, mid, right);
    }
}

Complexity

Time: $O(n\log n)$
Space: $O(n)$

---

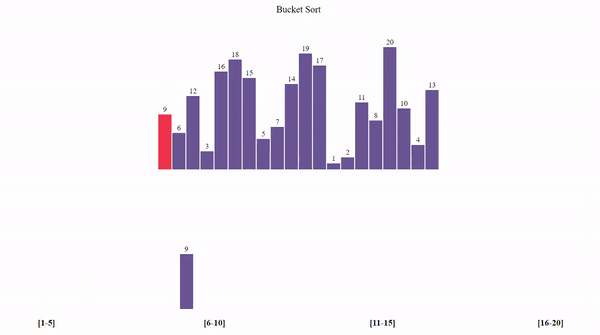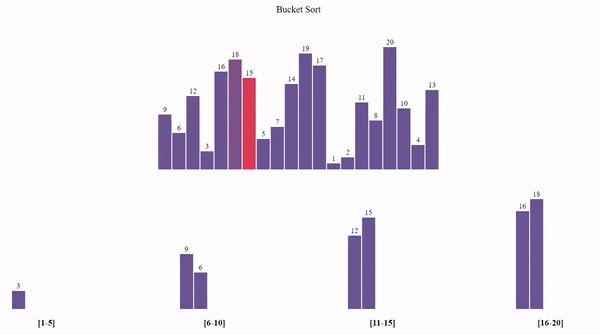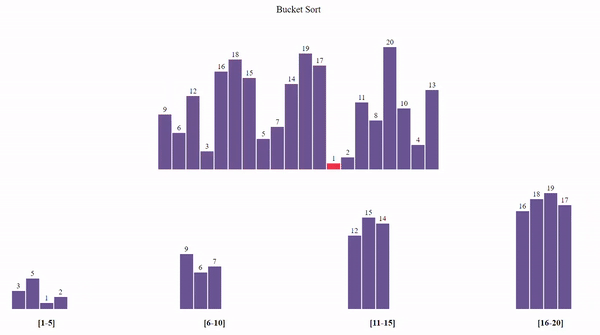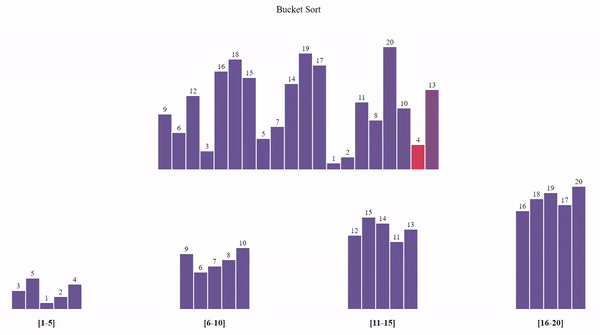
Bucket Sort

Bucket Sort distributes elements into buckets and sorts each bucket individually.

Steps

1. Divide the array into several buckets.
2. Sort each bucket individually.
3. Concatenate all buckets to form the sorted array.

Animation

C++ Implementation

#include <vector>
#include <algorithm>
using namespace std;
 
void bucketSort(vector<float>& arr) {
    int n = arr.size();
    vector<vector<float>> buckets(n);
 
    for (int i = 0; i < n; i++) {
        int idx = n * arr[i];
        buckets[idx].push_back(arr[i]);
    }
 
    for (int i = 0; i < n; i++) {
        sort(buckets[i].begin(), buckets[i].end());
    }
 
    int idx = 0;
    for (int i = 0; i < n; i++) {
        for (float val : buckets[i]) {
            arr[idx++] = val;
        }
    }
}

Complexity

Time: $O(n+k)$ (average), $O(n^2)$ (worst-case)
Space: $O(n+k)$

---

Radix Sort

Radix Sort sorts integers by processing individual digits.

Steps

1. Sort elements based on the least significant digit.
2. Move to the next significant digit and repeat.
3. Continue until the most significant digit.

Animation

C++ Implementation

#include <vector>
#include <algorithm>
#include <cmath>
using namespace std;
 
void countSort(vector<int>& arr, int exp) {
    vector<int> output(arr.size());
    int count[10] = {0};
 
    for (int num : arr)
        count[(num / exp) % 10]++;
 
    for (int i = 1; i < 10; i++)
        count[i] += count[i - 1];
 
    for (int i = arr.size() - 1; i >= 0; i--) {
        int digit = (arr[i] / exp) % 10;
        output[--count[digit]] = arr[i];
    }
 
    for (int i = 0; i < arr.size(); i++)
        arr[i] = output[i];
}
 
void radixSort(vector<int>& arr) {
    int maxVal = *max_element(arr.begin(), arr.end());
    for (int exp = 1; maxVal / exp > 0; exp *= 10) {
        countSort(arr, exp);
    }
}

Complexity

Time: $O(nk)$
Space: $O(n+k)$

---

Heap Sort

Heap Sort uses a binary heap structure to sort elements.

Steps

1. Build a max heap from the array.
2. Remove the root of the heap and reduce its size.
3. Heapify the root to maintain the heap property.

Animation

C++ Implementation

#include <vector>
#include <algorithm>
using namespace std;
 
void heapify(vector<int>& arr, int n, int i) {
    int largest = i;
    int left = 2 * i + 1;
    int right = 2 * i + 2;
 
    if (left < n && arr[left] > arr[largest])
        largest = left;
 
    if (right < n && arr[right] > arr[largest])
        largest = right;
 
    if (largest != i) {
        swap(arr[i], arr[largest]);
        heapify(arr, n, largest);
    }
}
 
void heapSort(vector<int>& arr) {
    int n = arr.size();
    for (int i = n / 2 - 1; i >= 0; i--)
        heapify(arr, n, i);
 
    for (int i = n - 1; i > 0; i--) {
        swap(arr[0], arr[i]);
        heapify(arr, i, 0);
    }
}

Complexity

Time: $O(n\log n)$
Space: $O(1)$

---

Insertion Sort

Insertion Sort builds the sorted array one element at a time by inserting elements into their correct position.

Steps

1. Iterate over the array from the second element.
2. Compare the current element with the elements to its left.
3. Insert the element into its correct position.
4. Repeat for the remaining elements.

Animation

C++ Implementation

#include <vector>
#include <algorithm>
 
void insertionSort(vector<int>& arr) {
    int n = arr.size();
    for (int i = 1; i < n; i++) {
        int key = arr[i];
        int j = i - 1;
        while (j >= 0 && arr[j] > key) {
            arr[j + 1] = arr[j];
            j--;
        }
        arr[j + 1] = key;
    }
}

#include <iostream>
 
int main() {
	cout << "test" << endl;
	return 0
}