Differential Equations in Neuroscience

study notes for a Artem Kirsanov video

Abstract

This video covers Dynamical Systems Theory, and how it can be used to model the behavior of systems in which time is a factor.

Looking at a Neuron, how can we apply this?

Graphic

Neurons are temporal computers. Unlike the contrary, neurons don’t only have “inputs” and “outputs” as factors, but also what that neuron was doing 1 millisecond ago, 1 second ago, or even minutes before.

This is exactly what Dynamical Systems Theory is all about. This will cover differential equations, limit cycles, equilibrium points, and phase portraits.

We will learn the fundamentals in this note, and later apply it to Neuronal Dynamics

State Variables

At its core, Dynamical Systems Theory is about studying things that change. This can be anything from a neuron firing, to a population of bacteria, or even a leaf floating in the water.

Warning

The KEY is having a way to describe the system state at any given point.

This is where state variables come into play. We use state variables to track the most important aspects of a phenomena. They will be real numbers used to fully describe the state of a system.

Let’s take an example of a ball in motion

Example

A ball is in motion within a 3d plane of existence. What are its state variables?

Solution

Motion in the 3D requires 6 variables:

3 for the Position Vector of the ball, x,y,z

3 for the Velocity/Direction Vector of the ball, also x,y,z

Graphic

But this can range depending both on what you are examining, but also on what you ACTUALLY care about. Let’s explain

Example

State variables can range, even for objects that we would consider to be in a 3d space.

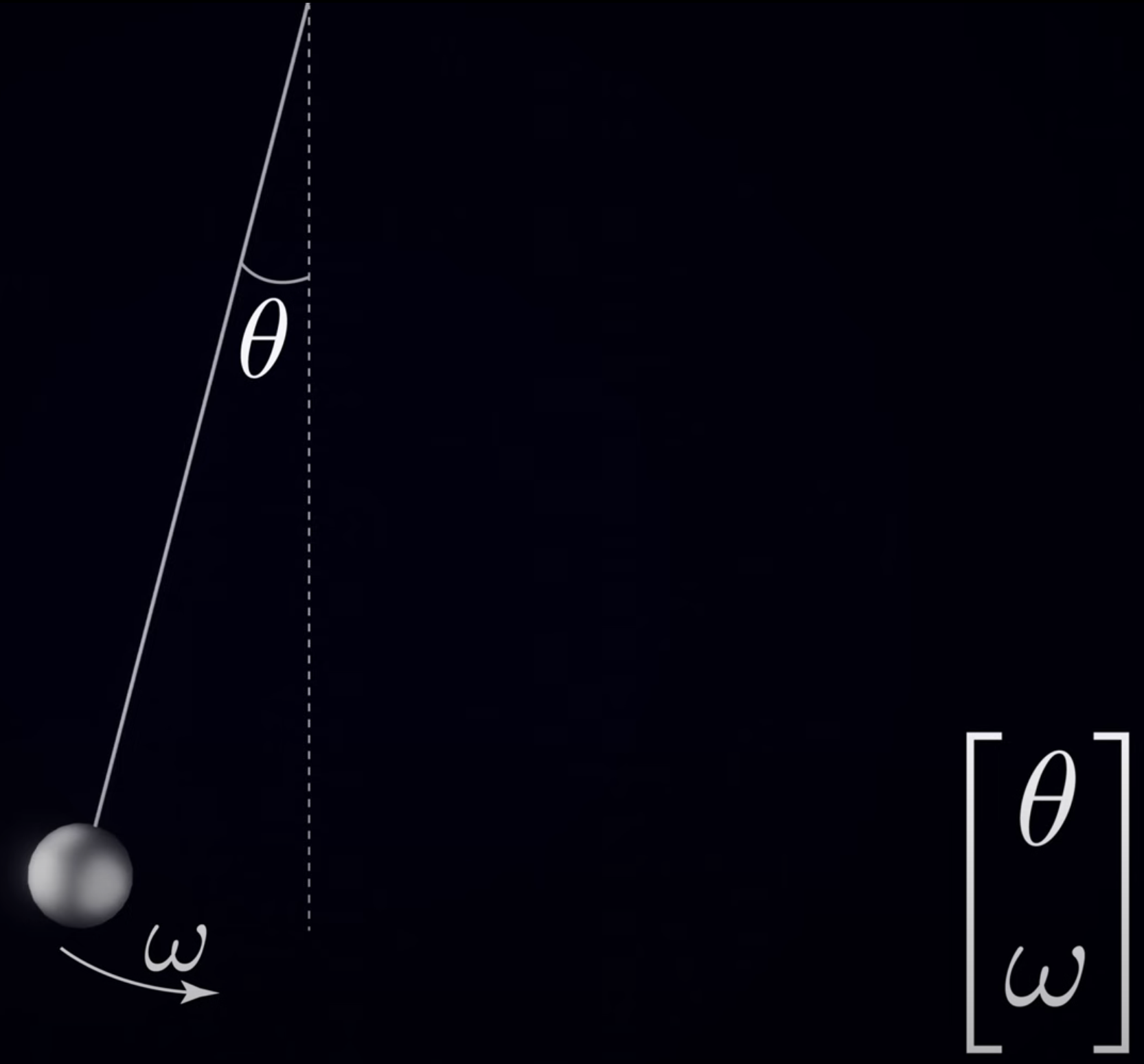
Like the ball in motion, a pendulum has some observed motion over time, but what state variable do we actually care about?

Well it turns out we only really need 2, if we only care about observing the “important” repeating motion of the pendulum that we all know, even though it also has a direction and postion vector like the ball.

Graphic

where $θ$ is the angle away from center and $ω$ is its direction/velocity in a said direction, single dimension

The importance of this is that even though there might be other state variables that we can account for in our calculations, it is oftentimes unnecessary for what we are trying to find. And for extremely complex systems like neurons, it is vital to make sure we are only observing the state variables that matter to us.

A neuroscientist observing the electrical properties of neurons might choose completely different state variables than, for example a biochemist would when observing the sugar content within, or the DNA being repaired.

We will talk about the actual state variables we use for neuroscience a bit later, but for now, let’s introduce the formalism of the differential equations themselves.

Here’s a sample of the equations to come:

C_{m} \frac{d V _{m}}{d t} I_{K^{+}} I_{N a^{+}} I_{l} = \sum I_{i o n} = g_{K} n^{4} (E_{K} - V_{m}) = g_{N a} m^{3} h (E_{N a} - V_{m}) = g_{l} (E_{l} - V_{m})