CH7 - Discrete Random Variables

Discusses the concept of discrete random variables and their probability distributions.

---

What is a Discrete Random Variable?

Discrete outcomes are those that can be counted and are distinct from one another. A discrete random variable is a variable that can take on a finite number of values. For example, the number of heads in a series of coin flips is a discrete random variable.

This differs from continuous random variables, which can take on any value within a range. For example, the height of a person is a continuous random variable.

We can model a discrete random variables outcomes through a binomial distribution, which describes the probability of getting a certain number of successes in a fixed number of trials.

Python

import matplotlib.pyplot as plt import numpy as np # Create figure with two subplots side by side fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 4)) # Discrete example: Coin flips outcomes = [0, 1, 2, 3, 4] probabilities = [0.0625, 0.25, 0.375, 0.25, 0.0625] # Binomial probabilities for 4 flips ax1.bar(outcomes, probabilities, width=0.5) ax1.set_title('Discrete: Number of Heads in 4 Coin Flips') ax1.set_xlabel('Number of Heads') ax1.set_ylabel('Probability') # Continuous example: Height distribution x = np.linspace(150, 190, 100) y = np.exp(-((x - 170)**2)/(2*100)) / (np.sqrt(2*np.pi*100)) # Normal distribution ax2.plot(x, y) ax2.fill_between(x, y, alpha=0.3) ax2.set_title('Continuous: Height Distribution') ax2.set_xlabel('Height (cm)') ax2.set_ylabel('Probability Density') plt.tight_layout() plt.show()

Output

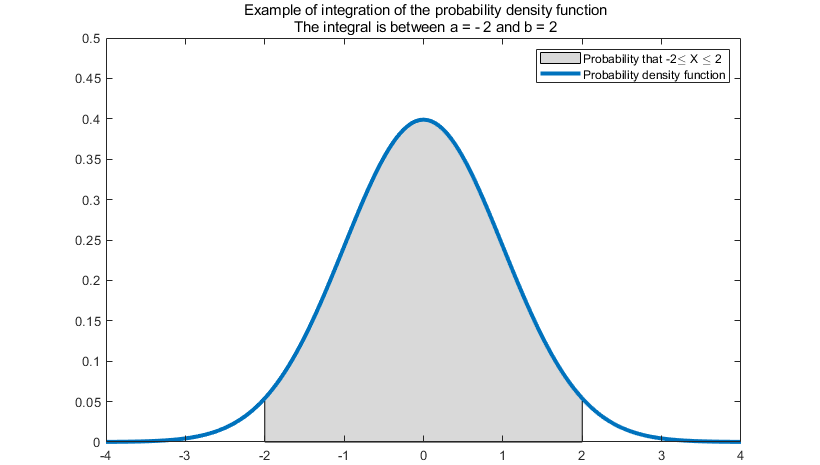
Continuous Random Variables

Continuous Random Variables are those that can take on any value within a range. For example, the height of a person is a continuous random variable.

To contrast, a continuous random variable has a infinitely dividable range of values, with “infinite precision”

---

There is a lot more to cover on what we can do with these random variables, but I already have several notes written for another class, namely CH2 - Random Variables.