Homework 2 - DFA and NFA Construction

Abstract

This document the formal definitions and constructs for 3 primary DFAs/NFAs, with two extra considered for extra credit. We seek to prove that a language is regular by providing a DFA that recognizes it.

IMPORTANT NOTE: My image rendered is currently a bit broken, and will sometimes jump a page(will rewrite myself soon). For now, refer to figure caption to match images to their respective location.

---

Definitions

We define a DFA/NFA as a 5 tuple:

$$M=\left(Q,\sum ,\delta ,q_0,F\right)$$

Where:

• $Q$ is a finite set of states
• $\sum$ is a finite set of symbols
• $\delta :Q\times \sum \to Q$ is the transition function
• $q_0\in Q$ is the start state
• $F\subseteq Q$ is the Set of accepting states

---

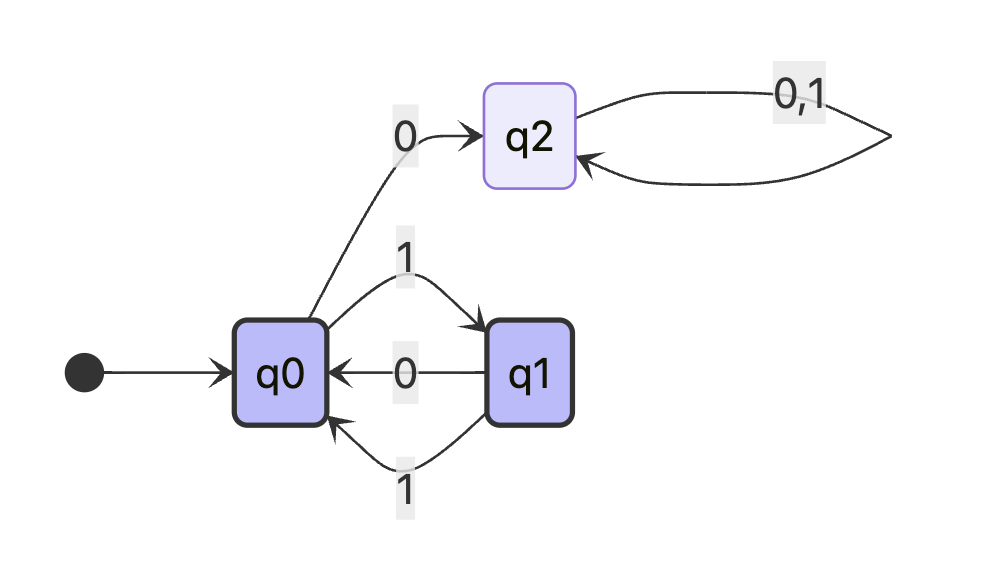
Problem 1

Construct a DFA that recognizes the language:

$$\{w\mid weveryoddpositionofwisa1\}$$

Provide a formal definition and a state diagram. $\sum =\{0,1\}$

Formal Definition

States

$$Q=\{q_0,q_1,q_2\}$$

• $q_0$ is state where next symbol is odd position
• $q_1$ is state where next symbol is even position
• $q_2$ is the sink state for all error

Language/Alphabet

$$\sum =\{0,1\}$$

Transition Function $\delta$

$\delta$	$0$	$1$
$q_0$	$q_2$	$q_1$
$q_1$	$q_0$	$q_0$
$q_2$	$q_2$	$q_2$

Start State

$$q_0$$

Accepting States

$$F=\{q_0,q_1\}$$

State Diagram

provided by mermaid

• white dot is start state entry point
• highlighted state is accepted state

see figure 1

---

Problem 2

For any string $w=w_1{w}_2\dots w_n$, the reverse of w, written $w^{\mathcal{R}}$, is the string $w$ in reverse order, $w_n\dots w_2{w}_1$. For any language $A$, let $A^{\mathcal{R}}=\{w^{\mathcal{R}}\mid w\in A\}$.

Prove that if $A$ is regular, so is $A^{\mathcal{R}}$. For this, consider how, starting with any arbitrary NFA to recognize $A$, you’d modify the NFA to recognize $A^{\mathcal{R}}$. Once you have the idea, write a recipe that would work for any NFA.

Idea / Goal

We are looking to show that when $A$ is regular, so is $A^{\mathcal{R}}$. Suppose $A$ is an NFA that:

$$N=\left\{Q,\sum ,\delta ,q_0,F\right\}$$

Where this NFA can be represented as $L(N)=A$. We want to create an NFA that recognizes $A^{\mathcal{R}}$

Construction

We define this new NFA as $M^{\prime }$:

$$M^{\prime }=\left(Q^{\prime },\sum ^{\prime },{\delta }^{\prime },q_0^{\prime },F^{\prime }\right)$$

It remains relatively unchanged compared to the original, except for a few key differences:

• we add a new state, $q_{new}$ to the states set $Q$, where $Q^{\prime }=Q\cup \{q_{new}\}$, which is essentially the new entry point for the NFA
• we add a new accept state, which is now $\{q_0\}$
• we reverse the transitions in the transition function:
  • if $p$ can transition to $q$ through $a$, then we reverse the transition $q{\to }^{a}p$
  • new transition function should look something like:

$${\delta }^{\prime }(p,(fora))=\{q\in Q^{\prime }\mid ptoqthrougha\}forallp$$

where “p to q through a” is representing $p{\to }^{a}q$

• epsilon transition is added for the new start state to the next state in line $f$:

$$q_{new}{\to }^{ϵ}f$$

Formal Definition

We now define the NFA $M^{\mathcal{R}}=\left(Q^{\prime },{\sum }^{\prime },{\delta }^{\prime },q_{new},F^{\prime }\right)$ with the following:

States:

States $Q^{\prime }$ is $Q$ and $q_{new}$ which is $\to$ $Q^{\prime }=Q\cup q_{new}$

Alphabet/Finite Set of Symbols:

Alphabet stays the same as $\sum$ so just treat it as such

Transition Function

$${\delta }^{\prime }(p,a)=\{q\in Q^{\prime }\mid p\in \delta (q,a)\}$$

where new start state is $q_0$ taking path of $ϵ$

Start State

New start state is $q_{new}$

Accept States

For this theoretical NFA, the accept state is $q_0$

Reason This Works

This works for this example, as in the original NFA, we use a string w that is accepted if there is such path from $q_0$ to a state $f$ in $F$ that is labeled by w. When all the transitions are reversed, any of these paths now become f to $q_0$ labeled by the modified w, $w^{\mathcal{R}}$.

We have to add a new start state $q_{new}$ with the transition $ϵ$ for the states $f$ in $F$ because we need to allow the automaton to “start” at any of the original accept states for it to be truly reversed.

The new accepting condition comes by finding if there is a string $s$ that $M^{\mathcal{R}}$ can take from $q_{new}$ to $q_0$ that is labeled as $s$. Essentially, there needs to be some path in $M$ from $q_0$ to some $f$ in $F$ that is labeled by the inverse, $s^{\mathcal{R}}$. So: $s=w^{\mathcal{R}}$ for this point $w$ in $A$.

For this reason, $M^{\mathcal{R}}$ can recognize $A^{\mathcal{R}}$ exactly.

Constructing a DFA. for $A^{\mathcal{R}}$

Using this we can effectively reverse any NFA to an equivalent DFA ( using our rules of subset construction, etc ), to ensure that there is a DFA that can recognize $A^{\mathcal{R}}$ as required $\square$

All we need to do is take the NFA $M$ for $A$, find $M^{\mathcal{R}}$ for $A^{\mathcal{R}}$ by reversing all transitions, creating new start state epsilon transition to original accept states, and making sure that the original start state is only accept state.

We can convert this to a DFA if we want to, but we know how to do this with subset construction.

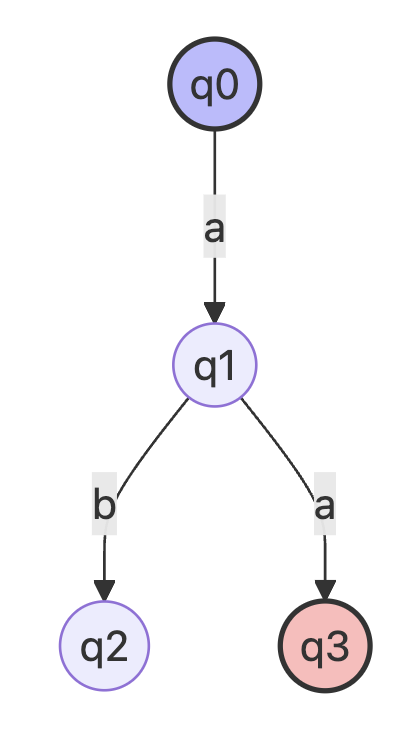
Example of Reversing NFA

Original NFA $M$:

see figure 2

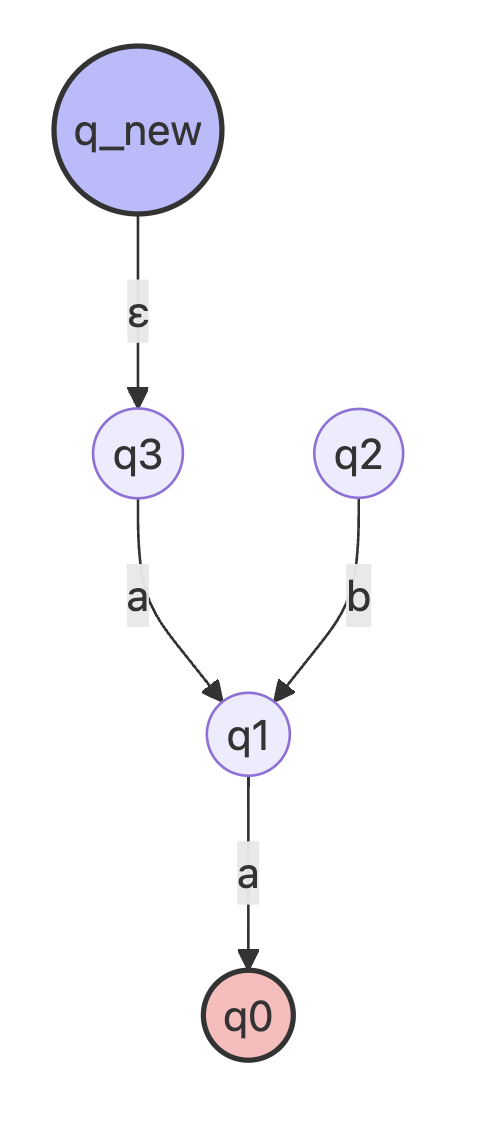
Reversed NFA $M^{\mathcal{R}}$ with new entry point $q_{new}$

see figure 3

---

Problem 3

Let $B_n=\{a^k\mid kisamultipleofn\}$. Show that for each $n\ge 1$, the language $B_n$ is regular.

Hint: Construct the base case for $n=1$ and then construct a DFA for $n=2$ and notice what changes. Then use what you learned to complete the proof.

Hint: If you really get stuck, and you’ve already produced state diagrams for the $n=1$ and $n=2$ cases, try producing a state diagram for the $n=3$ case and consider what changes when going from $n=2$ to $n=3$.

Given/Goal

We are looking to prove that for every time $n\ge 1$, language

$$B_n=\{a^k\mid kisamultipleofn\}$$

is a regular language.

We can do this by constructing a DFA that will recognize it. We are looking to count the occurrences of $a$ in modulo $n$.

Cases

We have cases $1\dots 3$ to go through, so we will construct a state diagram for each one

Base Case $n=1$

For $n=1$, we know that all non negative integers are multiples of 1, so:

$$B_1=\{a^k\mid k\ge 0\}=a^{\ast }$$

This is a very simple DFA, with only a single state that is both the start and the accepting.

see figure 4

Case $n=2$

When $n=2$, we get:

$$B_2=\{a^k\mid kisamultipleof2\}$$

This means that the language consists of all strings that have an even number of $a$‘s.

For this we only need two states:

• $q_0:$ all $a$ we have seen is even
• $q_1:$ all $a$ we have seen i odd

Transitions for these two should be:

• $q_0$ points to $q_1$ when $a$ received
• $q_1$ points to $q_0$ when $a$ received

see figure 5

Case $n=3$

When $n=3$ we get:

$$B_3=\{a^k\mid kisamultipleof3\}$$

Which represents when the strings received have a number of $a$‘s that is divisible by 3

This DFA consists of 3 states:

• $q_0:$ when remainder is 0, multiple of 3
• $q_{1:}$ when remainder is 1 when $÷3$
• $q_2:$ when remainder is 2 when $÷3$

The transitions for these states are as follows:

• $q_0$ points to $q_1$ when a received
• $q_1$ points to $q_2$ when a received
• $q_2$ points to $q_0$ when a received

see figure 6

Expanding This out to All case $n\ge 1$

For any amount $n\ge 1$, we can construct a DFA with states:

$$q_0,q_1,\dots ,q_{n-1}$$

• $q_0$ will always be the start and accepting state
• amount of states is dictated by number of $n-1$

We can define a transition function for this relation with the following:

$$\delta (q_i,a)=q_{(i+1)}\mathrm{mod}n$$

Essentially, we can conclude that for any number $n$ we can construct a finite automaton with a regular pattern.

Thus, $B_n$ is a regular language for all $n\ge 1$ as required $\square$

---

Extra Credit Problem A

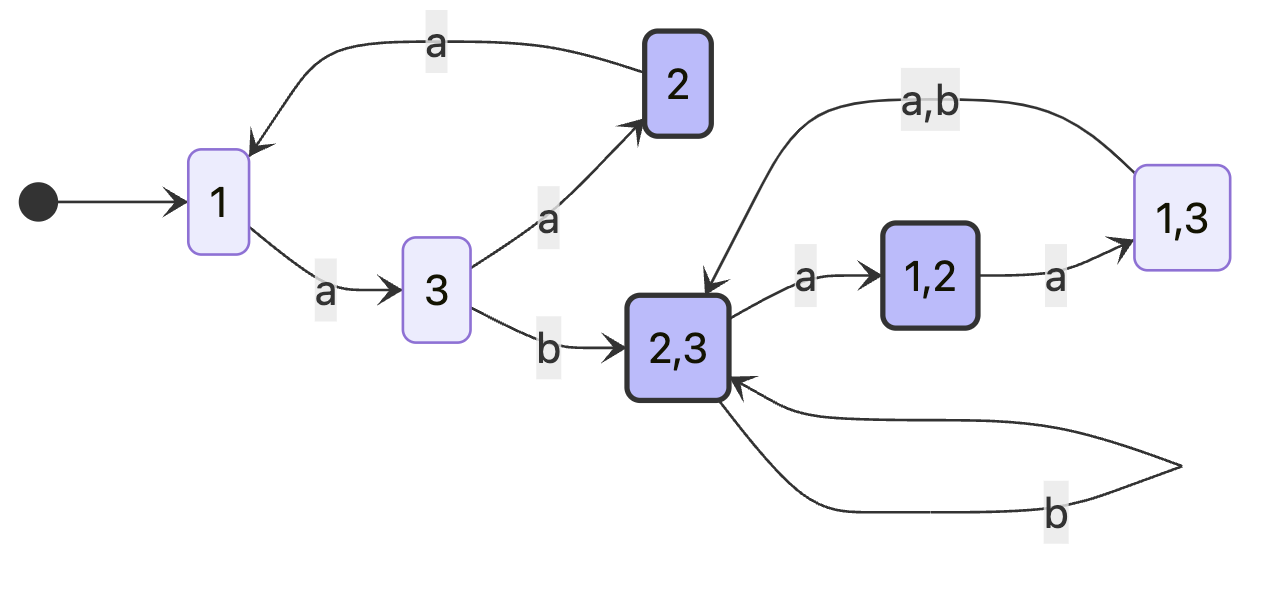
Convert the following NFA to an equivalent DFA. For subset construction, follow the recipe provided by Sipser Theorem 1.39 and the corresponding proof (as presented in class). Leave your construction unpruned, but be sure to indicate any unnecessary or unreachable states in the DFA thus constructed, if any.

see figure 7

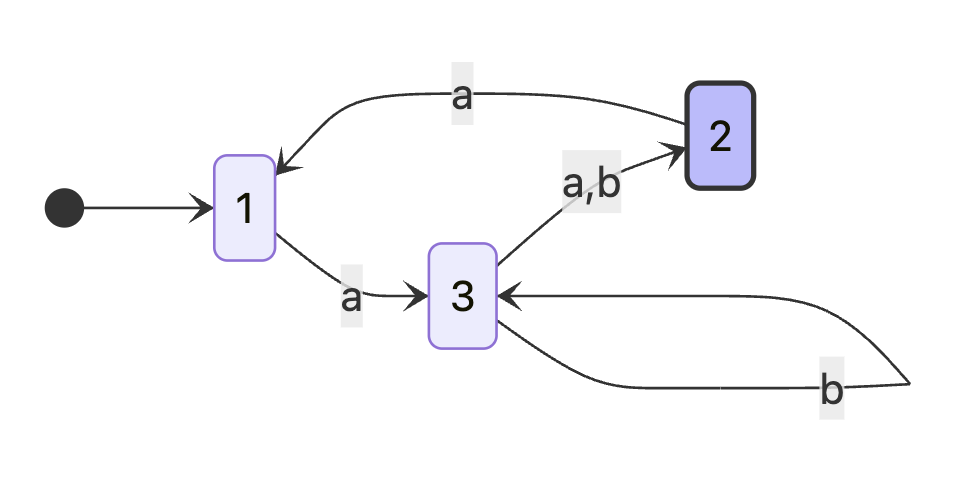
Listing Transitions

For state 1:

$$\delta (1,a)=\{3\}$$

and has no b transition

For state 2:

$$\delta (2,a)=\{1\}$$

For state 3:

$$\delta (3,a)=\{2\}$$ $$\delta (3,b)=\{3,2\}$$

since the b route goes to 2 and 3

Defining New DFA

1. We define the start state as $\{1\}$
2. Going from $\{1\}$ to:
   • $a$: $\delta (1,a)=\{3\}$
   • $b$: $\delta (1,b)=\{\varnothing \}$
3. Going from $\{3\}$ to:
   • $a$: $\delta (3,a)=\{2\}$
   • $b$: $\delta (3,b)=\{3,2\}$
4. Going from $\{2\}$ to: ( note we define this as accept state )
   • $a$: $\delta (2,a)=\{1\}$
   • $b$: $\delta (2,b)=\{\varnothing \}$
5. Going from $\{2,3\}$ to: ( also contains accept state )
   • $a$: $\delta (2,a)\cup \delta (3,a)=\{1,2\}$
   • $b$: $\delta (2,b)\cup \delta (3,b)=\varnothing \cup \{3,2\}\to \{3,2\}$
6. Going from $\{1,2\}$ to: (also contains accept state )
   • $a$: $\delta (1,a)\cup \delta (2,a)=\{1,3\}$
   • $b$: $\delta (1,b)\cup \delta (2,b)=\varnothing \cup \varnothing \to \varnothing$
7. Going from $1,3$ to:
   • $a$: $\delta (1,a)\cup \delta (3,a)=\{2,3\}$
   • $b$: $\delta (1,b)\cup \delta (3,b)=\varnothing \cup \{2,3\}\to \{2,3\}$
8. For Dead States $\varnothing$:
   • for $a$ and $b$: $\delta (\varnothing ,b)=\{\varnothing \}$

Constructing Table Of Transitions

DFA State	On $a$	On $b$	Accepting
$\{1\}$	$\{3\}$	$\varnothing$	No
$\{3\}$	$\{2\}$	$\{2,3\}$	No
$\{2\}$	$\{1\}$	$\varnothing$	Yes
$\{2,3\}$	$\{1,2\}$	$\{2,3\}$	Yes
$\{1,2\}$	$\{1,3\}$	$\varnothing$	Yes
$\{1,3\}$	$\{2,3\}$	$\{2,3\}$	No
$\varnothing$	$\varnothing$	$\varnothing$	No

Note:

I could be wrong, but it seems as though all states are reachable here, so no pruning would be needed even if we wanted to.

Constructing the DFA

Defining a DFA for:

$$M=\left(Q,\sum ,\delta ,q_0,F\right)$$

• States: $\{1\},\{3\},\{2\},\{2,3\},\{1,2\},\{1,3\},\varnothing$
• Alphabet: $\{a,b\}$
• Start State: $1$
• Accepting States: $\{2\},\{2,3\},\{1,2\}$
• Transitions:
  • 1 goes to 3 and $\varnothing$
  • 3 goes to 2 and 2,3
  • 2 goes to 1 and $\varnothing$
  • 2,3 goes to 1,2 and 2,3
  • 1,2 goes to 1,3 and $\varnothing$
  • 1,3 goes to 2,3 and 2,3
  • $\varnothing$ goes to $\varnothing$ and $\varnothing$

Diagram

provided by mermaid

see figure 8