16.4 Green's Theorem

Let $C$ be a simple closed curve and let $\mathcal{D}$ be the region bounded by $C$. We say $C$ has positive orientation if $C$ is traversed in the counterclockwise direction.

Positive Orientation

$\mathcal{D}$ is always on your left as you traverse the curve

Negative Orientation

$\mathcal{D}$ is always on your right as you traverse the curve

---

Abstract

Green's Theorem (named for George Green):

Let $\mathcal{D}$ be a simply connected region whose boundary curve $C$ is a simple, closed, positively oriented curve. If $P(x,y)$ and $Q(x,y)$ have continuous first-order partials on some open region containing $\mathcal{D}$, then:

$${\int }_{C}P(x,y)dx+Q(x,y)dy={\int }_{\mathcal{D}}\int \left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)dA$$

This theorem says that under certain conditions, we can evaluate a line integral as a double integral.

---

Remarks

1. To use this theorem correctly, note that $C$ must have positive orientation. If $C$ has negative orientation, we have to multiply our answer by $-1$:

$${\int }_C\cdots =-{\int }_{-C}\cdots =-{\int }_{\mathcal{D}}\int (Q_x-P_y)dA$$

2. We can state the theorem more succinctly as:

$${\oint }_{\partial \mathcal{D}}\vec{F}\cdot d\vec{r}={\int }_{\mathcal{D}}\int (Q_x-P_y)dA$$

• The notation "$\partial \mathcal{D}$" means “boundary curve of $\mathcal{D}$“. So, $\partial \mathcal{D}=C$.
• $\partial \mathcal{D}$ is a closed curve, so we use the $\oint$ notation (recall this is called a circulation integral).
• If $\vec{F}=⟨P(x,y),Q(x,y)⟩$, the integrand says:

$$\vec{F}\cdot d\vec{r}=⟨P,Q⟩\cdot dx,dy⟩=Pdx+Qdy$$

which is the form we used on the previous page.

---

Proving Green’s Theorem

We will prove this for the special case where $\mathcal{D}$ is a simple region, meaning a region which is simultaneously Type I and Type II. We wish to show:

$${\oint }_{\partial d}\vec{F}\cdot d\vec{r}={\oint }_{\partial \mathcal{D}}Pdx+Qdy={\int }_{\mathcal{D}}\int (Q_x-P_y)dA$$

We will do this by showing:

$${\oint }_{\partial \mathcal{D}}Pdx=-{\int }_{\mathcal{D}}{P}_{y}dAAND{\oint }_{\partial \mathcal{D}}Qdy={\int }_{\mathcal{D}}{Q}_{x}dA(\ast )$$

The result will follow by linearity of the integral.

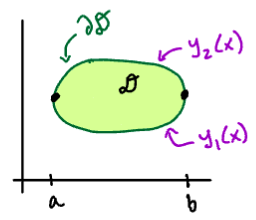
Let $\mathcal{D}$ be a simple region with positively-oriented boundary curve $\partial \mathcal{D}$. Consider the case where we view $\mathcal{D}$ as a Type I region:

Sketch

$\mathcal{D}$ as a Type I region

Sketch

$\partial \mathcal{D}$ decomposed into $\partial \mathcal{D}-C_1\cup C_2$

We compute the first expression in (*) directly as:

$${\oint }_{\partial \mathcal{D}}Pdx={\int }_{C_1}Pdx+{\int }_{C_2}Pdx={\int }_{C_1}Pdx-{\int }_{-C_2}Pdx(\ast \ast )$$

( The “negation” trick will help us soon. ) We can parameterize $C_1$ and $-C_2$ by:

$$C_1:⟨t,y_1(t)⟩t\in [a,b]$$ $$C_2:⟨t,y_2(t)⟩t\in [a,b]$$

(**) is then:

$$\begin{array}{rl}{\oint }_{\partial \mathcal{D}}Pdx& ={\int }_a^{b}P(t,y_1(t))dt-{\int }_a^{b}P(t,y_2(t))dt\\ & =-{\int }_a^{b}P(t,y_2(t))-P(t,y_1(t))dt\\ & =-{{\int }_a^{b}P(t,y)|}_{y=y_1(t)}^{y=y_2(t)}dt\\ & =-{\int }_a^b{\int }_{y_1(t)}^{y_2(t)}{P}_y(t,y)dydt\\ & =-{\int }_a^b{\int }_{y_1(x)}^{y_2(x)}{P}_y(x,y)dydx\\ & =-{\int }_{\mathcal{D}}\int P_y(x,y)dA\end{array}$$

This is exactly what we wanted in (*). The other expression in (*) can be obtained by regarding $\mathcal{D}$ as a Type II region.

---

Finding Area with Green’s Theorem

Recall that the area of region $\mathcal{D}$ can be found by:

$$Area(\mathcal{D})={\int }_{\mathcal{D}}\int 1dA$$

Green’s Theorem says that:

$${\oint }_{C}Pdx+Qdy={\int }_{\mathcal{D}}\int Q_x-P_{y}dA$$

So, if we can find functions $Q_x$ and $P_y$ satisfying $Q_x-P_y=1$, then we can “reverse” Green’s Theorem and find area by computing a line integral.

There are several ways to “force” $Q_x-P_y=1$:

$$Q=x,P=0\to A={\oint }_{c}xdy$$ $$Q=0,P=-y\to A=-{\oint }_{c}ydx$$ $$Q=\frac{1}{2}x,P=-\frac{1}{2}y\to A=\frac{1}{2}{\oint }_{c}xdy-ydx$$